Page 5 - KIV - Álgebra 3

Álgebra 3° Secundaria

1. Si
A×B={(3;2), (3;3), (3;5), (5;2); (5;3), (5;5)}
Calcular: B – A

A) {2} B) {1;3} C) {1; 2; 3}
D) { } E) {1; 2}

2. Si (2x+y; 3x–2y)=(9; 3), hallar x+y

A) 3 B) 6 C) 7
D) 7 E) 10

3. Determina la relación R en los conjuntos
A={1; 3; 5} y B={2; 3; 6} siendo
R={(a:b) ∈ A×B/ b=2a} indique n(R)

A) 1 B) 2 C) 3
D) 4 E) 5

4. Sea la función A) f, g B) g, h C) f, g, h
f={(1;7), (3;4), (5;7), (3;3y–5), (1;2x+1)} D) f, m E) Solo h
hallar x+y
9. De las siguientes relaciones, ¿cuáles no son
A) 4 B) 5 C) 7 funciones?
D) 9 E) 6 F = {(4;4), (5;5), (6;6)}
G = {(3;4), (4;4), (5;4), (6;4)}
5. Dada la función: f={(1;2), (2;3), (3;4)}, H = {(5;2), (5;3), (5;6)}
calcular f(3)+2f(1)+f(f(1)) I = {(4;3), (3;4), (5;2) (2;5)}

A) 9 B) 7 C) 5 A) H B) H y I C) I
D) 8 E) 11 D) F y I E) F y G

6. Sea: A={2 /x ∈ z; 0 ≤ x ≤ 3} y 10. Determine el valor de: f(129), si f={(2;5),
x
R={(a, b) ∈ A /a+b= impar}. Colocar (V) o (F) (–1;3), (2;2a–b), (–1;b–a), (a+b ;a)} es una
2
2
I. (1; 16) ∈ R función.
II. (4; 1), (8;1) ∈ R
III. (32; 1) ∉ R A) 8 B) 27 C) 19
IV. n(R)= 10 D) 1 E) 16

A) VFFV B) FFFF C) FFVV
D) VVVV E) VVFF 11. Dada la función

7. Dada la función, con x < 0
3
2
G={(3;7), (4;3), (4; x –x+1)}, hallar x –5

A) 3 B) –6 C) 3 y – 6
D) 8 E) 6

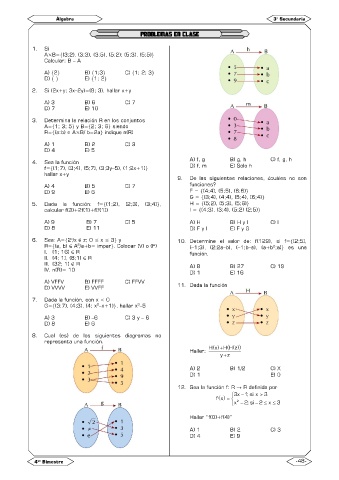
8. Cual (es) de los siguientes diagramas no
representa una función.
 
H   x  H H z
Hallar:
y z


A) 2 B) 1/2 C) X
D) 1 E) 0

12. Sea la función f: R → R definida por
3x 1; si x  3

 
f   x  

2
  x  2; si 2  x  3

Hallar “f(0)+f(4)”

A) 1 B) 2 C) 3
D) 4 E) 9

4 Bimestre -48-
to