Page 6 - UNI M2 Geometria 5to sec

Geometría 5° UNI

11. En un triángulo ABC obtuso en B, la mediatriz de III. Dos triángulos rectángulos soperimétricos
BC interseca a AC en M, tal que AM=2(MN), N siempre son congruentes.
)
es punto medio de BC y m ABC = 2 ( m ACB .
Calcule m ACB. A) VVV B) FFF C) FVV
D) FVF E) VFF
A) 30° B) 40° C) 45°
D) 50° E) 36° 17. En el triángulo ABC se traza la ceviana interior
BM, de modo que AM=BM+BC. Si la
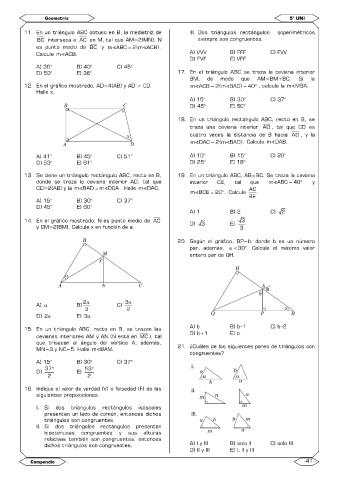
12. En el gráfico mostrado, AD=4(AB) y AD > CD. m ACB = 2 ( m BAC ) = 40 , calcule la m MBA.

Halle x.
A) 15° B) 30° C) 37°
D) 45° E) 60°

18. En un triángulo rectángulo ABC, recto en B, se
traza una ceviana interior AD , tal que CD es
cuatro veces la distancia de B hacia AD , y la
)
m DAC = 2 (m BAD . Calcule m DAB.

A) 41° B) 45° C) 51° A) 10° B) 15° C) 20°
D) 53° E) 61° D) 25° E) 18°

13. Se tiene un triángulo rectángulo ABC, recto en B, 19. En un triángulo ABC, AB=BC. Se traza la ceviana
donde se traza la ceviana interior AD, tal que interior CE, tal que m = ABC  40 y
CD=2(AB) y la m BAD = m DCA . Halle m DAC. AC
m = BCE  20 . Calcule BE .
A) 15° B) 30° C) 37°
D) 45° E) 60°
A) 1 B) 2 C) 2
14. En el gráfico mostrado, N es punto medio de AC D) 3 E) 3
y CM=2(BM). Calcule x en función de a. 3

20. Según el gráfico, BP=b, donde b es un número
par, además,  <30°. Calcule el máximo valor
entero par de QH.

2  3 
A)  B) C)
3 2
D) 2 E) 3

15. En un triángulo ABC, recto en B, se trazan las A) b B) b–1 C) b–2
cevianas interiores AM y AN (N está en MC ), tal D) b+1 E) b
que trisecan al ángulo del vértice A; además,
MN=3 y NC=5. Halle m BAM. 21. ¿Cuáles de los siguientes pares de triángulos son
congruentes?
A) 15° B) 30° C) 37°
37  53 
D) E)
2 2

16. Indique el valor de verdad (V) o falsedad (F) de las
siguientes proposiciones.

I. Si dos triángulos rectángulos isósceles
presentan un lado de común, entonces dichos
triángulos son congruentes.
II. Si dos triángulos rectángulos presentan
hipotenusas congruentes y sus alturas
relativas también son congruentes, entonces
dichos triángulos son congruentes. A) I y III B) solo II C) solo III
D) II y III E) I, II y III

Compendio -41-