Page 35 - UNI M4 Trigonometría_Neat

Trigonometría 5° UNI

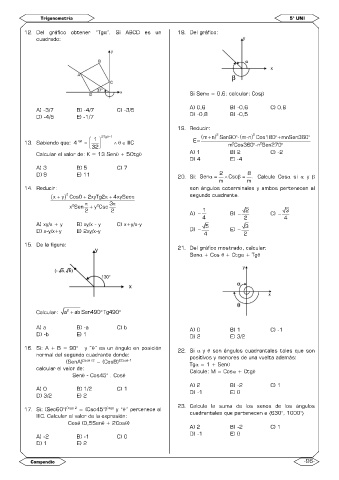
12. Del gráfico obtener “Tgα”. Si ABCD es un 18. Del gráfico:
cuadrado:

Si Sen = 0,6; calcular: Cos

A) -3/7 B) -4/7 C) -3/5 A) 0,6 B) -0,6 C) 0,8
D) -4/5 E) -1/7 D) -0,8 B) -0,5

19. Reducir: 2 2
(
)
)
 1  2Tg− 1 E= ( m+n Sen90°- m-n Cos180°+mnSen360°
13. Sabiendo que: 4 Tg =      IIIC m Cos360°-n Sen270°
2
2
 32
Calcular el valor de: K = 13 Sen + 5Ctg A) 1 B) 2 C) -2
D) 4 E) -4
A) 3 B) 5 C) 7
D) 9 E) 11 20. Si: Sen = 2  Csc = 8 . Calcule Cos si  y 
m m
14. Reducir: son ángulos coterminales y ambos pertenecen al
(x + ) y 2 Cos0 + 2xyTg2 + 4xySec segundo cuadrante.
 3 
2
2
x Sen + y Csc
2 2 A) − 1 B) − 2 C) − 3
4 2 4
A) xy/x + y B) xy/x - y C) x+y/x-y 5 3
D) x-y/x+y E) 2xy/x-y D) − 4 E) − 2

15. De la figura:
21. Del gráfico mostrado, calcular:
Sen + Cos  + Ctg + Tg


Calcular: a + ab Sen490 Tg490
2

A) a B) -a C) b A) 0 B) 1 C) -1
D) -b E) 1 D) 2 E) 3/2

16. Si: A + B = 90° y “” es un ángulo en posición 22. Si  y  son ángulos cuadrantales tales que son
normal del segundo cuadrante donde: positivos y menores de una vuelta además:
(SenA) Csc+2 = (CosB) 2Csc-1 Tg = 1 + Sen
calcular el valor de: Calcule: M = Cos + Ctg
Sen - Cos45° . Cos
A) 2 B) -2 C) 1
A) 0 B) 1/2 C) 1 D) -1 E) 0
D) 3/2 E) 2
23. Calcule la suma de los senos de los ángulos
17. Si: (Sec60°) Ctg-2 = (Csc45°) Ctg y “” pertenece al cuadrantales que pertenecen a 〈630°, 1000°〉
IIIC. Calcular el valor de la expresión:
Cos (0,5Sen + 2Cos)
A) 2 B) -2 C) 1
A) -2 B) -1 C) 0 D) -1 E) 0
D) 1 E) 2

Compendio -96-