Page 159 - Avanzado-Ambiente y salud_Unidad 2_texto 1°_ciclo avanzado

Operando con funciones

La función lineal es importante porque es el punto de partida para modelar el
comportamiento de la naturaleza. Existen situaciones en la vida real que se pueden
modelar linealmente y así dar un valor estimado de la variable dependiente (y)
para un cierto valor de la variable independiente (x).

La modelación de la función lineal es un gráfica lineal, el cual se representa en el
plano cartesiano. ¿Sabes que una función afín? ¿Cuál es la diferencia entre una
función lineal y una función afín, si ambas tienen la misma representación?

Primero determinemos sus características similares:

§ Las dos se representan por una recta que pasa por un punto.

§ Las dos tienen una variable independiente (x) y una variable dependiente (y).
§ Las dos se usan para expresar relaciones entre dos magnitudes en la vida
cotidiana.

Ahora determinemos en que se diferencian:

Función lineal En cuanto a: Función Afín
Las variables no
Las variables son
Proporcionalidad son directamente
directamente proporcionales
proporcionales
Pasa por el origen de Gráfica No pasa por el origen de
coordenadas coordenadas

y = mx Expresión algebraica y = mx +n

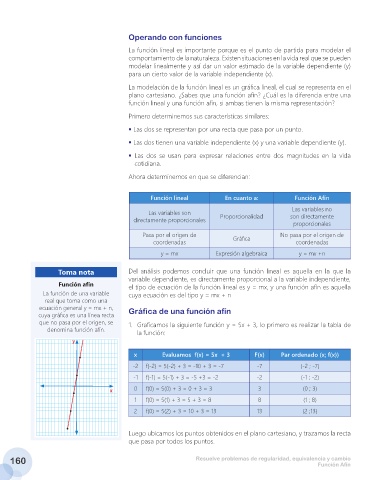
Toma nota Del análisis podemos concluir que una función lineal es aquella en la que la
variable dependiente, es directamente proporcional a la variable independiente,
Función afín
el tipo de ecuación de la función lineal es y = mx, y una función afín es aquella
La función de una variable cuya ecuación es del tipo y = mx + n
real que toma como una
ecuación general y = mx + n, Gráfica de una función afín
cuya gráfica es una línea recta
que no pasa por el origen, se 1. Graficamos la siguiente función y = 5x + 3, lo primero es realizar la tabla de
denomina función afín.
la función:
y

x Evaluamos f(x) = 5x + 3 F(x) Par ordenado (x; f(x))
-2 f(-2) = 5(-2) + 3 = -10 + 3 = -7 -7 (-2 ; -7)
-1 f(-1) = 5(-1) + 3 = -5 +3 = -2 -2 (-1 ; -2)

x 0 f(0) = 5(0) + 3 = 0 + 3 = 3 3 (0 ; 3)
1 f(0) = 5(1) + 3 = 5 + 3 = 8 8 (1 ; 8)
2 f(0) = 5(2) + 3 = 10 + 3 = 13 13 (2 ;13)

Luego ubicamos los puntos obtenidos en el plano cartesiano, y trazamos la recta
que pasa por todos los puntos.

160 Resuelve problemas de regularidad, equivalencia y cambio
Función Afín