Page 162 - Avanzado-Ambiente y salud_Unidad 2_texto 1°_ciclo avanzado

En el recorrido de los cuatro amigos al inicio de la experiencia de aprendizaje,
se observa que los desplazamientos son diferentes, formando diferentes Toma nota
representaciones en el plano cartesiano, denotándose a su vez diferentes ángulos
de inclinación. En la vida real, cuando vamos por la calle, encontramos terrenos Intercepto y pendiente
en desnivel, a veces totalmente recta y horizontal, de repente la calle empieza a Intercepto: Es el valor de “y”
“subir” verticalmente. A esta inclinación se le llama pendiente. ¿Qué diferencias cuando “x” vale cero. Es decir el
punto donde la recta cruza al
encuentras en las siguientes graficas?
eje vertical (y).

m: pendiente es la inclinación
que la recta tiene respecto del
eje de abscisas.

-
∆y y y
m = = 2 1
-
∆x x x
2 1
n: coeficiente de posición es
Función dreciente Función drececiente Función constante el valor en el cual la recta corta
al eje de las ordenadas.
Como observan en las graficas los angulos de inclianción son diferentes, entonces
tienen diferentes pendientes.
f(x) = mx + n
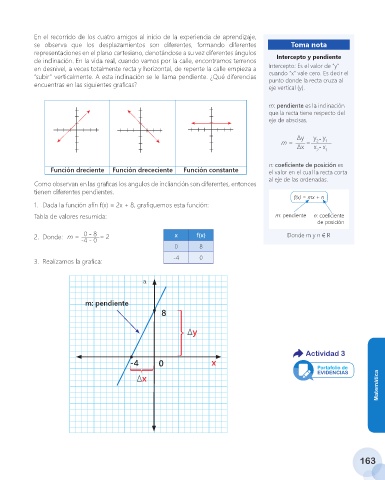
1. Dada la función afín f(x) = 2x + 8, grafiquemos esta función:
Tabla de valores resumida: m: pendiente n: coeficiente
de posición

2. Donde: m = 0 - 8 = 2 x f(x) Donde m y n ϵ R
-4 - 0
0 8
-4 0
3. Realizamos la grafica:

a.

m: pendiente
8

∆y

Actividad 3
-4 0 x
Portafolio de
EVIDENCIAS
Matemática
∆x

163