Page 5 - KII - Geometria

Geometría 3° Secundaria

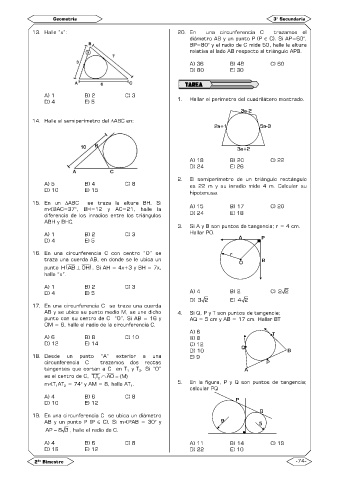
13. Halle “x”: 20. En una circunferencia C trazamos el
diámetro AB y un punto P (P ∈ C). Si AP=60°,
BP=80° y el radio de C mide 50, halle la altura
relativa al lado AB respecto al triángulo APB.

A) 36 B) 48 C) 60
D) 80 E) 30

A) 1 B) 2 C) 3
D) 4 E) 5 1. Hallar el perímetro del cuadrilátero mostrado.

14. Halle el semiperímetro del ABC en:

A) 18 B) 20 C) 22
D) 24 E) 26

2. El semiperímetro de un triángulo rectángulo
A) 5 B) 4 C) 8 es 22 m y su inradio mide 4 m. Calcular su
D) 10 E) 15 hipotenusa.

15. En un ABC se traza la altura BH. Si
mBAC=37°, BH=12 y AC=21, halle la A) 15 B) 17 C) 20
diferencia de los inradios entre los triángulos D) 24 E) 18
ABH y BHC.
3. Si A y B son puntos de tangencia; r = 4 cm.
A) 1 B) 2 C) 3 Hallar PO.
D) 4 E) 5

16. En una circunferencia C con centro “O” se
traza una cuerda AB, en donde se le ubica un
punto  AB  OH  . Si AH = 4x+3 y BH = 7x,
H
halle “x”.

A) 1 B) 2 C) 3
D) 4 E) 5 A) 4 B) 2 C) 2 2
D) 3 2 E) 4 2
17. En una circunferencia C se traza una cuerda
AB y se ubica su punto medio M, se une dicho 4. Si Q, P y T son puntos de tangencia;
punto con su centro de C “O”. Si AB = 16 y AQ = 5 cm y AB = 17 cm. Hallar BT
OM = 6, halle el radio de la circunferencia C.
A) 6
A) 6 B) 8 C) 10 B) 8
D) 12 E) 14 C) 12
D) 10
18. Desde un punto “A” exterior a una E) 9
circunferencia C trazamos dos rectas
tangentes que cortan a C en T y T . Si “O”
1
2
es el centro de C, T T  1 2 AO  {M}
mT AT = 74° y AM = 8, halle AT . 5. En la figura, P y Q son puntos de tangencia;
1
1
2
calcular PQ
A) 4 B) 6 C) 8
D) 10 E) 12

19. En una circunferencia C se ubica un diámetro
AB y un punto P (P ∈ C). Si mPAB = 30° y
AP  8 3 , halle el radio de C.

A) 4 B) 6 C) 8 A) 11 B) 14 C) 19
D) 16 E) 12 D) 22 E) 10

do
2 Bimestre -74-