Page 56 - u4

P2: OSO/OVY
P1: OSO/OVY
GO01962-Smith-v1.cls
UAE-Math-Grade-12-Vol-1-SE-718383-ch4
SECTION 4.4 • •
4-37 QC: OSO/OVY T1: OSO October 25, 2018 17:24 Increasing and Decreasing Functions 247
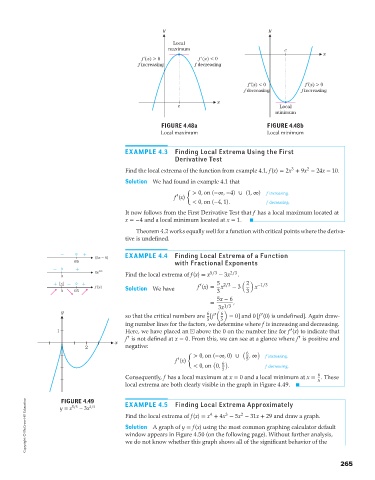
y y
Local
maximum c
x
f (x) > 0 f (x) < 0
f increasing f decreasing

f (x) < 0 f (x) > 0
f decreasing f increasing
x
c Local
minimum

FIGURE 4.48a FIGURE 4.48b
Local maximum Local minimum

EXAMPLE 4.3 Finding Local Extrema Using the First
Derivative Test
2
3
Find the local extrema of the function from example 4.1, f(x) = 2x + 9x − 24x − 10.
Solution We had found in example 4.1 that
{ > 0,on (−∞, −4) ∪ (1, ∞) f increasing.
′
f (x)
< 0,on (−4, 1). f decreasing.
It now follows from the First Derivative Test that f has a local maximum located at
x =−4 and a local minimum located at x = 1.
Theorem 4.2 works equally well for a function with critical points where the deriva-
tive is undefined.

- 0 + EXAMPLE 4.4 Finding Local Extrema of a Function
(5x - 6)
6/5 with Fractional Exponents
- 0 +
3x 1/3 5∕3 2∕3
0 Find the local extrema of f(x) = x − 3x .
2
+ × - 0 + ′ 5 2∕3 ( ) −1∕3
f (x) Solution We have f (x) = x − 3 x
0 6/5 3 3
= 5x − 6 ,
3x 1∕3
y ( )
6
′
so that the critical numbers are [f ′ 6 5 = 0] and 0 [f (0) is undefined]. Again draw-
5
ing number lines for the factors, we determine where f is increasing and decreasing.
′
1 Here, we have placed an × above the 0 on the number line for f (x) to indicate that
′
′
f is not defined at x = 0. From this, we can see at a glance where f is positive and
x
2 negative:
{ > 0,on (−∞, 0) ∪ ( 6 , ∞ ) f increasing.
′
f (x) 5
(
< 0,on 0, 6 ) . f decreasing.
5
6
Consequently, f has a local maximum at x = 0 and a local minimum at x = . These
local extrema are both clearly visible in the graph in Figure 4.49. 5
Copyright © McGraw-Hill Education y = x 5∕3 − 3x 2∕3 EXAMPLE 4.5 Finding Local Extrema Approximately
FIGURE 4.49
4
3
2
Find the local extrema of f(x) = x + 4x − 5x − 31x + 29 and draw a graph.
Solution A graph of y = f(x) using the most common graphing calculator default
window appears in Figure 4.50 (on the following page). Without further analysis,
we do not know whether this graph shows all of the significant behavior of the
265