Page 57 - u4

P1: OSO/OVY
GO01962-Smith-v1.cls
UAE-Math-Grade-12-Vol-1-SE-718383-ch4
CHAPTER 4 • •
Applications of Differentiation
248 P2: OSO/OVY QC: OSO/OVY T1: OSO October 25, 2018 17:24 4-38
y function. [Note that some fourth-degree polynomials (e.g., f(x) = x ) have graphs
4
that look very much like the one in Figure 4.50.] First, we compute
10
2
3
′
f (x) = 4x + 12x − 10x − 31.
′
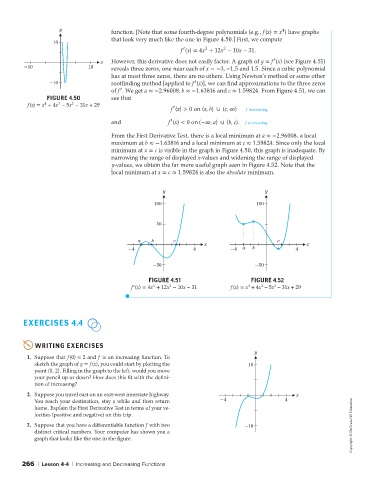
x However, this derivative does not easily factor. A graph of y = f (x) (see Figure 4.51)
-10 10 reveals three zeros, one near each of x =−3, −1.5 and 1.5. Since a cubic polynomial
has at most three zeros, there are no others. Using Newton’s method or some other
′
-10 rootfinding method [applied to f (x)], we can find approximations to the three zeros
′
of f .Weget a ≈−2.96008,b ≈−1.63816 and c ≈ 1.59824. From Figure 4.51, we can
FIGURE 4.50 see that
3
2
4
f(x) = x + 4x − 5x − 31x + 29 ′
f (x) > 0on(a, b) ∪ (c, ∞) f increasing.
′
and f (x) < 0 on (−∞,a) ∪ (b, c). f decreasing.
From the First Derivative Test, there is a local minimum at a ≈−2.96008, a local
maximum at b ≈−1.63816 and a local minimum at c ≈ 1.59824. Since only the local
minimum at x = c is visible in the graph in Figure 4.50, this graph is inadequate. By
narrowing the range of displayed x-values and widening the range of displayed
y-values, we obtain the far more useful graph seen in Figure 4.52. Note that the
local minimum at x = c ≈ 1.59824 is also the absolute minimum.
y y

100 100

50

a b c c
x x
-4 4 -4 a b 4

-50 -50

FIGURE 4.51 FIGURE 4.52
′
3
4
2
3
2
f (x) = 4x + 12x − 10x − 31 f(x) = x + 4x − 5x − 31x + 29
EXERCISES 4.4

WRITING EXERCISES
y
1. Suppose that f(0) = 2 and f is an increasing function. To
sketch the graph of y = f(x), you could start by plotting the 10
point (0, 2). Filling in the graph to the left, would you move
your pencil up or down? How does this fit with the defini-
tion of increasing?
2. Suppose you travel east on an east-west interstate highway. x
You reach your destination, stay a while and then return -4 4
home. Explain the First Derivative Test in terms of your ve-
locities (positive and negative) on this trip.
3. Suppose that you have a differentiable function f with two -10 Copyright © McGraw-Hill Education
distinct critical numbers. Your computer has shown you a
graph that looks like the one in the figure.

266 | Lesson 4-4 | Increasing and Decreasing Functions