Page 55 - u4

P1: OSO/OVY
GO01962-Smith-v1.cls
UAE-Math-Grade-12-Vol-1-SE-718383-ch4
CHAPTER 4 • •
Applications of Differentiation
246 P2: OSO/OVY QC: OSO/OVY T1: OSO October 25, 2018 17:24 4-36
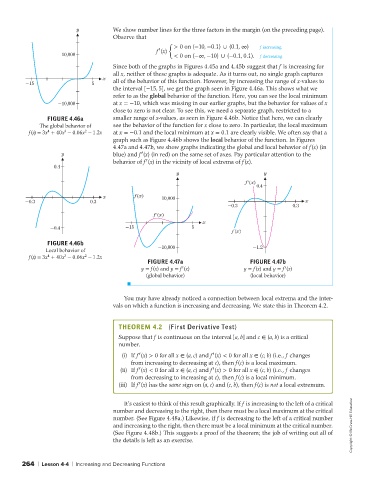
y We show number lines for the three factors in the margin (on the preceding page).
Observe that
{ > 0on(−10, −0.1) ∪ (0.1, ∞) f increasing.
′
f (x)
10,000 < 0on(−∞, −10) ∪ (−0.1, 0.1). f decreasing.
Since both of the graphs in Figures 4.45a and 4.45b suggest that f is increasing for
all x, neither of these graphs is adequate. As it turns out, no single graph captures
x all of the behavior of this function. However, by increasing the range of x-values to
-15 5
the interval [−15, 5], we get the graph seen in Figure 4.46a. This shows what we
refer to as the global behavior of the function. Here, you can see the local minimum
-10,000 at x =−10, which was missing in our earlier graphs, but the behavior for values of x
close to zero is not clear. To see this, we need a separate graph, restricted to a
FIGURE 4.46a smaller range of x-values, as seen in Figure 4.46b. Notice that here, we can clearly
The global behavior of see the behavior of the function for x close to zero. In particular, the local maximum
2
4
3
f(x) = 3x + 40x − 0.06x − 1.2x at x =−0.1 and the local minimum at x = 0.1 are clearly visible. We often say that a
graph such as Figure 4.46b shows the local behavior of the function. In Figures
4.47a and 4.47b, we show graphs indicating the global and local behavior of f(x) (in
′
y blue) and f (x) (in red) on the same set of axes. Pay particular attention to the
′
behavior of f (x) in the vicinity of local extrema of f(x).
0.4
y y
f '(x)
0.4
x f (x) 10,000
-0.3 0.3 x
-0.3 0.3
f '(x)
x
-0.4 -15 5
f (x)
FIGURE 4.46b
Local behavior of -10,000 -1.2
2
3
4
f(x) = 3x + 40x − 0.06x − 1.2x
FIGURE 4.47a FIGURE 4.47b
′
′
y = f(x) and y = f (x) y = f(x) and y = f (x)
(global behavior) (local behavior)
You may have already noticed a connection between local extrema and the inter-
vals on which a function is increasing and decreasing. We state this in Theorem 4.2.

THEOREM 4.2 (First Derivative Test)
Suppose that f is continuous on the interval [a, b] and c ∈ (a, b) is a critical
number.
′
′
(i) If f (x) > 0 for all x ∈ (a, c) and f (x) < 0 for all x ∈ (c, b) (i.e., f changes
from increasing to decreasing at c), then f(c) is a local maximum.
′
′
(ii) If f (x) < 0 for all x ∈ (a, c) and f (x) > 0 for all x ∈ (c, b) (i.e., f changes
from decreasing to increasing at c), then f(c) is a local minimum.
′
(iii) If f (x) has the same sign on (a, c) and (c, b), then f(c) is not a local extremum.
It’s easiest to think of this result graphically. If f is increasing to the left of a critical
number and decreasing to the right, then there must be a local maximum at the critical
number. (See Figure 4.48a.) Likewise, if f is decreasing to the left of a critical number
and increasing to the right, then there must be a local minimum at the critical number. Copyright © McGraw-Hill Education
(See Figure 4.48b.) This suggests a proof of the theorem; the job of writing out all of
the details is left as an exercise.

264 | Lesson 4-4 | Increasing and Decreasing Functions