Page 126 - Geogebra 6 van A tot Z
P. 126
GeoGebra 6 van A tot Z
6.7 Kansberekening bij de normale (Gauss) verdeling
6.7.1 Inleidend voorbeeld
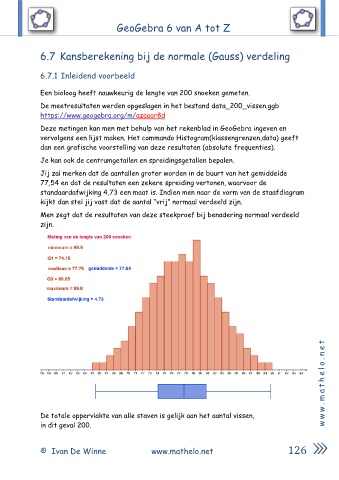
Een bioloog heeft nauwkeurig de lengte van 200 snoeken gemeten.
De meetresultaten werden opgeslagen in het bestand data_200_vissen.ggb
https://www.geogebra.org/m/azaaar8d
Deze metingen kan men met behulp van het rekenblad in GeoGebra ingeven en
vervolgens een lijst maken. Het commando Histogram(klassengrenzen,data) geeft
dan een grafische voorstelling van deze resultaten (absolute frequenties).
Je kan ook de centrumgetallen en spreidingsgetallen bepalen.
Jij zal merken dat de aantallen groter worden in de buurt van het gemiddelde
77,54 en dat de resultaten een zekere spreiding vertonen, waarvoor de
standaardafwijking 4,73 een maat is. Indien men naar de vorm van de staafdiagram
kijkt dan stel jij vast dat de aantal “vrij” normaal verdeeld zijn.
Men zegt dat de resultaten van deze steekproef bij benadering normaal verdeeld
zijn.
t
e
n
.
o
l
e
h
t
a
m
.
De totale oppervlakte van alle staven is gelijk aan het aantal vissen, w w
in dit geval 200. w
© Ivan De Winne www.mathelo.net 126