Page 128 - Geogebra 6 van A tot Z

GeoGebra 6 van A tot Z

Voorbeeld 1:

Een variabele is normaal verdeeld met μ = 7 en σ = 2
 Start GeoGebra en open een nieuw leeg werkblad.

 Typ in het invoerveld μ = 7 en ook σ = 2

 Typ in het invoerveld het voorschrift van de Gausskromme.

f(x) = 1 / (σ *sqrt(2*pi))*e^((-1 / 2)*((x - μ)/σ)^2)

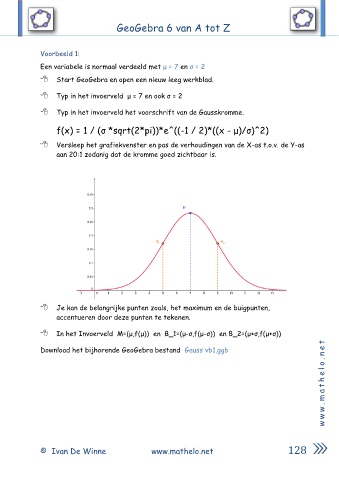
 Versleep het grafiekvenster en pas de verhoudingen van de X-as t.o.v. de Y-as
aan 20:1 zodanig dat de kromme goed zichtbaar is.

 Je kan de belangrijke punten zoals, het maximum en de buigpunten,
accentueren door deze punten te tekenen.

 In het Invoerveld M=(μ,f(μ)) en B_1=(μ-σ,f(μ-σ)) en B_2=(μ+σ,f(μ+σ))

t
Download het bijhorende GeoGebra bestand Gauss vb1.ggb e
n
. o
l
e
h
t a

m .
w
w

w

© Ivan De Winne www.mathelo.net 128