Page 130 - Geogebra 6 van A tot Z
P. 130
GeoGebra 6 van A tot Z
6.8 Onderzoeksvenster waarschijnlijkheidsrekenen
De oppervlakte gelegen onder de Gausskromme kan gebruikt worden om relatieve
frequenties bij de normale verdeling te benaderen.
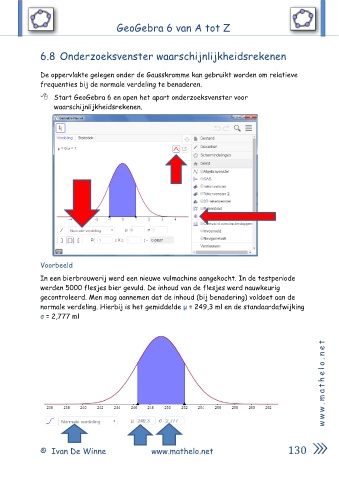
Start GeoGebra 6 en open het apart onderzoeksvenster voor
waarschijnlijkheidsrekenen.
Voorbeeld
In een bierbrouwerij werd een nieuwe vulmachine aangekocht. In de testperiode
werden 5000 flesjes bier gevuld. De inhoud van de flesjes werd nauwkeurig
gecontroleerd. Men mag aannemen dat de inhoud (bij benadering) voldoet aan de
normale verdeling. Hierbij is het gemiddelde μ = 249,3 ml en de standaardafwijking
σ = 2,777 ml
t
e
n
.
o
l
e
h
t
a
m
.
w
w
w
© Ivan De Winne www.mathelo.net 130