Page 160 - Geogebra 6 van A tot Z

GeoGebra 6 van A tot Z

8.7 Oppervlakken in 3D

Oppervlakken in een driedimensionale ruimte kunnen beschreven worden m.b.v. een
functie van twee veranderlijken f(x,y), met een parametervoorstelling, met een

impliciete vergelijking of met bol- of cilindercoördinaten.
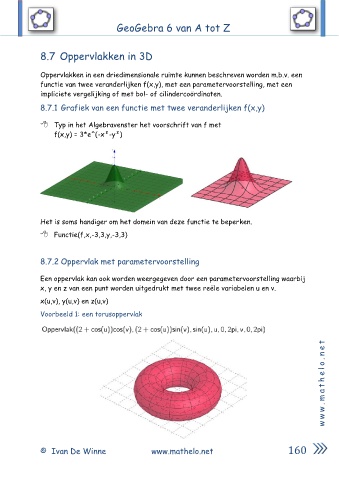
8.7.1 Grafiek van een functie met twee veranderlijken f(x,y)

 Typ in het Algebravenster het voorschrift van f met
f(x,y) = 3*e^(-x²-y²)

Het is soms handiger om het domein van deze functie te beperken.
 Functie(f,x,-3,3,y,-3,3)

8.7.2 Oppervlak met parametervoorstelling

Een oppervlak kan ook worden weergegeven door een parametervoorstelling waarbij
x, y en z van een punt worden uitgedrukt met twee reële variabelen u en v.

x(u,v), y(u,v) en z(u,v)

Voorbeeld 1: een torusoppervlak

t
e
n
.
o
l
e
h
t
a
m
.
w
w
w

© Ivan De Winne www.mathelo.net 160