Page 14 - HS 3 Regressie en correlatie
P. 14
Combinatieleer, kansrekening en verklarende statistiek
3.3.5 Eigenschappen van de correlatiecoëfficiënt
Wij hernemen het voorbeeld van de samenhang tussen de lengte en de schoenmaat van 10 jongens van
17 jaar.
Hieronder vind je de lengte en de schoenmaat van 10 jongens van 17 jaar.
Lengte in cm 166 170 168 175 175 180 189 192 195 151
Schoenmaat 37 39 38 39 41 40 44 44 45 34
In dit voorbeeld is de correlatiecoëfficiënt r = 0,98
Dit wijst op een sterke positieve correlatie tussen de lengte en de schoenmaat van de 10 jongens.
Men kan op een vrij eenvoudige manier met GeoGebra of Excel de correlatiecoëfficiënt berekenen.
Samenvatting
De correlatiecoëfficiënt heeft altijd een waarde tussen -1 en +1.
Indien r dicht bij 1 ligt, dan kan dit wijzen op een sterke tendens dat bij grote waarden voor de variabele
xi ook grote waarden voor yi overeenkomen en omgekeerd dat bij kleine waarden voor de variabele xi
ook kleine waarden voor yi overeenkomen.
Men spreekt dan over een sterke positieve lineaire correlatie.
Indien r dicht bij -1 ligt, dan kan dit wijzen op een sterke tendens dat bij kleine waarden voor de
variabele xi grote waarden voor yi overeenkomen en omgekeerd dat bij grote waarden voor de variabele
xi kleine waarden voor yi overeenkomen.
Men spreekt dan over een sterke negatieve lineaire correlatie.
Indien r dicht bij 1 ligt dan zullen de punten (xi , yi ) dicht aansluiten bij een rechte met een positieve
richtingscoëfficiënt.
Indien r dicht bij -1 ligt dan zullen de punten (xi , yi ) dicht aansluiten bij een rechte met een negatieve
richtingscoëfficiënt.
Opmerking
De correlatiecoëfficiënt drukt enkel en alleen de sterkte van een lineaire samenhang uit.
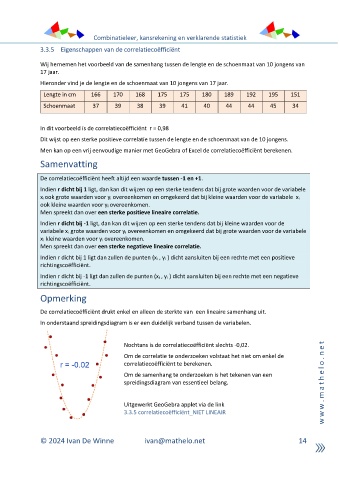
In onderstaand spreidingsdiagram is er een duidelijk verband tussen de variabelen.
Nochtans is de correlatiecoëfficiënt slechts -0,02. t
e
n
Om de correlatie te onderzoeken volstaat het niet om enkel de
.
correlatiecoëfficiënt te berekenen. o
l
Om de samenhang te onderzoeken is het tekenen van een e
h
spreidingsdiagram van essentieel belang. t
a
m
.
Uitgewerkt GeoGebra applet via de link w
3.3.5 correlatiecoëfficiënt_NIET LINEAIR w
w
© 2024 Ivan De Winne ivan@mathelo.net 14