Page 5 - Algemene sinusfunctie asin(bx+c) +d

GeoGebra in de derde graad

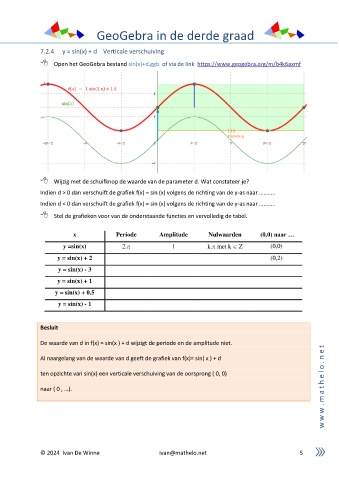
7.2.4 y = sin(x) + d Verticale verschuiving
 Open het GeoGebra bestand sin(x)+d.ggb of via de link https://www.geogebra.org/m/b4k6axmf

 Wijzig met de schuifknop de waarde van de parameter d. Wat constateer je?

Indien d > 0 dan verschuift de grafiek f(x) = sin (x) volgens de richting van de y-as naar ………..
Indien d < 0 dan verschuift de grafiek f(x) = sin (x) volgens de richting van de y-as naar ………..

 Stel de grafieken voor van de onderstaande functies en vervolledig de tabel.

x Periode Amplitude Nulwaarden (0,0) naar …
y =sin(x) 2. 1 k. met k  Z (0,0)

y = sin(x) + 2 (0,2)
y = sin(x) - 3

y = sin(x) + 1
y = sin(x) + 0.5

y = sin(x) - 1

Besluit

De waarde van d in f(x) = sin(x ) + d wijzigt de periode en de amplitude niet.
t
e
Al naargelang van de waarde van d geeft de grafiek van f(x)= sin( x ) + d n
.
o
ten opzichte van sin(x) een verticale verschuiving van de oorsprong ( 0, 0) l
e
h
naar ( 0 , …). t
a

m
. w
w
w

© 2024 Ivan De Winne ivan@mathelo.net 5