Page 6 - Algemene sinusfunctie asin(bx+c) +d

GeoGebra in de derde graad

7.2.5 De algemene sinusfunctie y = a.sin(b.x + c) + d met a > 0 en b > 0
 Open het GeoGebra bestand asin(bx+c)+d.ggb
of via de link https://www.geogebra.org/m/ecptmqcy
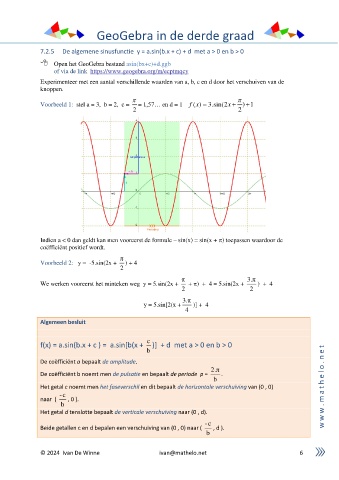
Experimenteer met een aantal verschillende waarden van a, b, c en d door het verschuiven van de
knoppen.
 
+
f x =
Voorbeeld 1: stel a = 3, b = 2, c = = 1,57… en d = 1 ( ) 3.sin(2x + ) 1
2 2

Indien a < 0 dan geldt kan men vooreerst de formule – sin(x) = sin(x + ) toepassen waardoor de
coëfficiënt positief wordt.
π
Voorbeeld 2: y = -5.sin(2x + ) + 4
2
π 3.π
We werken vooreerst het minteken weg y = 5.sin(2x + + ) + 4 = 5.sin(2x + ) + 4
2 2

3.π
y = 5.sin[2(x + )] + 4
4

Algemeen besluit

c
f(x) = a.sin(b.x + c ) = a.sin[b(x + )] + d met a > 0 en b > 0 t
b e
n
De coëfficiënt a bepaalt de amplitude. .
2.π o
De coëfficiënt b noemt men de pulsatie en bepaalt de periode p = . l
b e
h
Het getal c noemt men het faseverschil en dit bepaalt de horizontale verschuiving van (0 , 0) t
c - a
naar ( , 0 ). m
b .
Het getal d tenslotte bepaalt de verticale verschuiving naar (0 , d). w
w
c -
Beide getallen c en d bepalen een verschuiving van (0 , 0) naar ( , d ). w
b

© 2024 Ivan De Winne ivan@mathelo.net 6