Page 49 - Kalkulus Lanjut

Dengan   0 dan  −    2 . Persamaan permukaan diatas dapat ditulis sebagai

f
z = f(x,y) = (r cos ,r sin )  = f , (r ) 

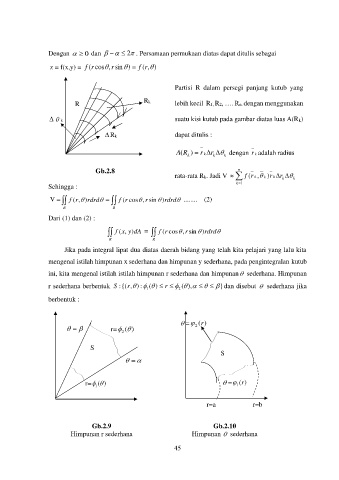
Partisi R dalam persegi panjang kutub yang

Rk
R lebih kecil R1, R2, …. Rn. dengan menggunakan

k suatu kisi kutub pada gambar diatas luas A(Rk)

Rk dapat ditulis :

A( R = r  
)
k r  dengan r adalah radius
k k k k

Gb.2.8 n

k r 
rata-rata Rk. Jadi V   f ( k r  ) k r 
,
k
k
Sehingga : k=1

V =  f ( r ) rdrd =  f ( r cos , r sin ) rdrd ........ (2)
,
R R

Dari (1) dan (2) :
 f ( x, y) dA =  f ( r cos , r sin ) rdrd
R R
Jika pada integral lipat dua diatas daerah bidang yang telah kita pelajari yang lalu kita
mengenal istilah himpunan x sederhana dan himpunan y sederhana, pada pengintegralan kutub

ini, kita mengenal istilah istilah himpunan r sederhana dan himpunan sederhana. Himpunan

r sederhana berbentuk S : {(r , : )  ( )  r   2 ( ),     }dan disebut  sederhana jika
1
berbentuk :

 = (r )
 =  r= ( ) 2
2

S
S
 = 

r= (  = 1 (r )

)
1

r=a r=b

Gb.2.9 Gb.2.10
Himpunan r sederhana Himpunan  sederhana

45