Page 55 - Linear Models for the Prediction of Animal Breeding Values 3rd Edition

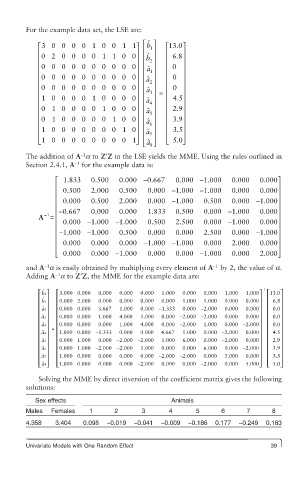
For the example data set, the LSE are:

⎡ 3 0000 1 0 0 1 1⎤ ⎡ ˆ ⎤ ⎡13.0⎤
b
1
⎢ ⎥ ⎢ ⎥ ⎢ ⎥
ˆ
⎢ 0 2 0000 11 00 ⎥ ⎢b ⎥ ⎢ 6.8 ⎥
2
⎢ 0 000000000⎥ ⎢ ⎥ ⎢ ⎢ 0 ⎥
ˆ a
⎢ ⎥ ⎢ 1⎥ ⎢ ⎥
⎢ 0 000000000 ⎥ ⎢ ˆ a 2 ⎥ ⎢ 0 ⎥
⎢ 0 000000000 ⎥ ⎢ ⎥ ⎢ 0 ⎥
3 = ⎢
⎢ ⎥ ⎢ ˆ a ⎥ ⎥
⎢ 10000 1 00000 ⎥ ⎢ ⎢ ˆ a ⎥ ⎢ 4.5 ⎥
⎢ 0 1 0000 1 000 ⎥ ⎢ 4 ⎥ ⎢ 2.9 ⎥
⎢ ⎥ ˆ a ⎢ 5 ⎥ ⎢ ⎥
⎢ 0 1 00000 1 0 0⎥ ⎢ ˆ a ⎥ ⎢ 3.9⎥
⎢ ⎥ ⎢ 6 ⎥ ⎢ ⎥
⎢ 10000000 1 0 ⎥ ⎢ ˆ a 7 ⎥ ⎢ 3.5 ⎥
⎢ ⎢ ⎣ 100000000 1⎥ ⎦ ⎢ ⎢ ⎣ 8⎦ ⎥ ⎥ ⎢ ⎣ 5.0⎥ ⎦
ˆ a
−1
The addition of A a to Z′Z in the LSE yields the MME. Using the rules outlined in
Section 2.4.1, A for the example data is:
−1
⎡ 1.833 0.500 0.000 − 0.667 0.000 − 1.000 0.000 0.000⎤
⎢ ⎥
⎢ 0.500 2.000 0 0.500 0.000 − 1.000 − 1.000 0.000 0.000 ⎥
⎢ 0.000 0.500 2.000 0.000 − 1.000 0.500 0.000 − 1.000⎥
0
⎢ ⎥
-1 ⎢ − 0.667 0.000 0.000 1.833 0.500 0.000 − 1.000 0.0000 ⎥
A = ⎢ 0.000 − 1.000 − 0.000 − ⎥
⎢ 1.000 0.500 2.500 1.000 0.000 ⎥
⎢ − 1.000 − 1.000 0 0.500 0.000 0.000 2.500 0.000 − 1.000 ⎥
⎢ 0.000 − 1.000 − ⎥
0
⎢ 0.000 0.000 1.000 0.000 2.000 0.000 ⎥
⎣ ⎢ 0.000 0.000 − 1.000 0.000 0.000 − 1.000 0.000 2.000⎥ ⎦
0
−1
−1
and A a is easily obtained by multiplying every element of A by 2, the value of a.
−1
Adding A a to Z′Z, the MME for the example data are:
⎡ b1⎤ ⎡ 3.000 0.000 0.000 0.000 0.000 1.000 0.000 0.000 1.000 1.000⎤ ⎡ 13.0⎤
1
−1
ˆ
ˆ ⎢
b1⎥ ⎢ 0.000 2..000 0.000 0.000 0.000 0.000 1.000 1.000 0.000 0.000⎥ ⎢ 6.8⎥
⎢ ⎥ ⎢ 0.000 0.000 3.6667 1.000 0.000 − 1.333 0.000 − 2.000 0.000 0.000 ⎥ ⎢ 0.0 ⎥
⎢ ⎥ ⎢ ⎥ ⎢ ⎥
ˆ a1
⎢ ⎥ ⎢ 0.000 0.000 1.000 4.0000 1.000 0.000 − 2.000 − 2.000 0.000 0.000 ⎥ ⎢ 0.0 ⎥
ˆ a2
⎢ ⎥ = ⎢ 0.000 0.000 0.000 1.000 4.0000 0.000 − 2.000 1.000 0.000 − 2.000 ⎥ ⎢ 0.0 ⎥
ˆ a3
⎢ ˆ a4 ⎥ ⎢ 1.000 0.000 − 1.333 0.000 0.000 4.6667 1.000 0.000 − 2.000 0.000 ⎥ ⎢ 4.5 ⎥
⎢ ˆ a5⎥ ⎢ 0.000 1.000 0.000 − 2.000 − 2.000 1.000 6..000 0.000 − 2.000 0.000⎥ ⎢ 2.9⎥
⎢ ˆ a6 ⎥ ⎢ 0.000 1.000 − 2.000 − 2.000 1.000 0.000 0.000 6 6.000 0.000 − 2.000 ⎥ ⎢ 3.9 ⎥
⎢ ⎥ ⎢ 0.000 − 2.000 − ⎥ ⎢ ⎥
ˆ a7
⎢ ⎥ ⎢ 1.000 0.000 0.000 0.000 2.000 0.000 0 5.000 0.000 ⎥ ⎢ 3.5 5 ⎥
⎣ ⎦ ⎣ 1.000 0.000 0.000 0.000 − 2.000 0.000 0.000 − 2.000 0.000 0 5.000 ⎦ ⎣ 5.0 ⎦
ˆ a8
Solving the MME by direct inversion of the coefficient matrix gives the following
solutions:
Sex effects Animals
Males Females 1 2 3 4 5 6 7 8
4.358 3.404 0.098 −0.019 −0.041 −0.009 −0.186 0.177 −0.249 0.183
Univariate Models with One Random Effect 39