Page 13 - MODUL_Persamaan_Trigonometri_Kelas_XI_SM-dikonversi

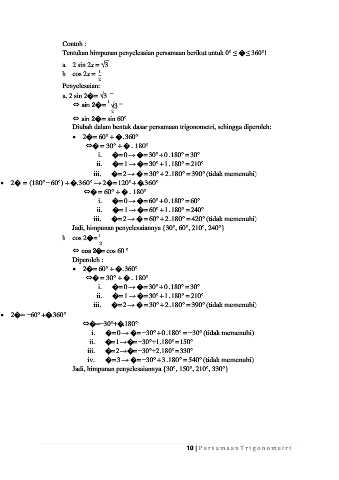
Contoh :
Tentukan himpunan penyelesaian persamaan berikut untuk 0° ≤ � ≤ 360°!
a. 2 sin 2x = √3
1
b. cos 2x =
2
Penyelesaian:
a. 2 sin 2� = √3
1
⇔ sin 2� = √3
2
⇔ sin 2� = sin 60°
Diubah dalam bentuk dasar persamaan trigonometri, sehingga diperoleh:
 2� = 60° + � . 360°
⇔� = 30° + � . 180°
i. � = 0 → � = 30° + 0 . 180° = 30°
ii. � = 1 → � = 30° + 1 . 180° = 210°
iii. � = 2 → � = 30° + 2 .180° = 390° (tidak memenuhi)
 2� = (180° − 60°) + �.360° → 2� = 120° + �.360°
⇔� = 60° + � . 180°
i. � = 0 → � = 60° + 0 . 180° = 60°
ii. � = 1 → � = 60° + 1 . 180° = 240°
iii. � = 2 → � = 60° + 2 .180° = 420° (tidak memenuhi)
Jadi, himpunan penyelesaiannya {30°, 60°, 210°, 240°}
1
b. cos 2� =
2

⇔ cos 2�= cos 60 °
Diperoleh :
 2� = 60° + � . 360°
⇔� = 30° + � . 180°
i. � = 0 → � = 30° + 0 . 180° = 30°
ii. � = 1 → � = 30° + 1 . 180° = 210°
iii. � = 2 → � = 30° + 2 .180° = 390° (tidak memenuhi)
 2� = −60° +�.360°
⇔�=−30°+�.180°
i. � = 0 → � = −30° + 0 .180° = −30° (tidak memenuhi)
ii. �= 1 →�= −30°+1.180° = 150°
iii. �= 2 →�= −30°+2.180° = 330°
iv. � = 3 → � = −30° + 3 .180° = 540° (tidak memenuhi)
Jadi, himpunan penyelesaiannya {30°, 150°, 210°, 330°}

10 | P e r s a m a a n T r i g o n o m e t r i