Page 85 - mathematics first

ُ
ً
ً
:ٍ ةيهتنم ريغ اهنم ايأو ةيهتنم ةعومجم اهنم ايأ دّ دح َّ مث ِ ةيلاتلا ِ تاعومجملا َ رصانع ْ بتكا ُ (3( لاثم
i) A =} x : 3 نم رغصأو -3 نمربكأ حيحص ددع x }
ٌ
A = } -2 , -1 , 0 , 1 , 2 { ٌ ةيهتنم ةعومجم يه نذإ ةسمخ ةعومجملا رصانع ددع
ii) B =} x ∈ Z : x > 6{ 6 نم ربكأ حيحص ددع x

B =} 7, 8 ,9 , 10 ,11 , …{ ةيهتنم ريغ ةعومجم يه نذإ ةعومجملا رصانع ددع ديدحت نكميلا

A=}- 4, -3, -2,-1,0,1,2 ,3 ,4{ , B = }-3, -1,0 ,2{ , C= }-4, -2, 4, 6 {تناك اذإ (4( لاثم

.ببسلا ركذ عم ؟لا مأ A ةعومجملا نم ةيئزج ةعومجم B ، C نم لك نأ له ْ نِّ يب
B ⊆ A A ىلا يمتني B ىلا يمتني رصنع لك نلأ A نم ةيئزج ةعومجم B

C ⊆ A A ىلا يمتنيلاو C ىلا يمتني 6 رصنعلا نلأ A نم ةيئزج ريغ ةعومجم C

Operations On Sets ِ تاعومجملا ىلع ُ تايلمعلا ]4-1-3[

ُ
. B ةعومجملاو A ِ ةعومجملا ىلإ يمتنت اهُ رصانع يتلا ةعومجملا يه B , A نيتعومجملا عطاقت ةعومجم
ِ
A ∩ B = } x : x ∈ A and x ∈ B{ :يتلآاك عطاقتلا ِ ةعومجم نع ُ رِّ بعنو
ِ
. B ةعومجملا وأ A ةعومجملا ىلإ يمتنت اهرصانع يتلا ةعومجملا يه B , A نيتعومجملا داحتا ةعومجم
ُ
A ∪ B = } x : x ∈ A or x ∈ B{ :يتلآاك ِ داحتلاا ِ ةعومجم نع ُ رِّ بعنو

A= }a, b , c , d ,e ,f ,g, h{ , B = }b, d, e,f, k, m{ , C= }a, g, h, n{ تناك اذإ (5( لاثم

i) A ∩ B ii) B ∩ C iii) B∩ A iv) B∪ C v) C∪B :دجوأف

i) A∩ B = }a, b , c , d ,e ,f ,g, h{ ∩}b, d, e,f, k, m{ = }b , d , e , f{

ii) B ∩ C = }b, d, e,f, k, m{ ∩}a, g, h, n{ = ∅

iii) B ∩A = } b ,d ,e , f { نأ ظحلا A ∩ B = B ∩A عطاقتلا ِ ةيلمعل لادبلإا ىمست ُ
ِ
iv) B ∪ C = }b, d, e,f, k, m{ ∪ }a, g, h, n{ = }b , d , e, f , k m ,a ,g ,h ,n{

v) C ∪ B = }b , d , e, f , k, m ,a ,g ,h ,n{
ْ
ُ
ِ داحتلاا ِ ةيلمعل لادبلإا ىمست B∪ C = C ∪ B نأ ظحلا

A= }-7 , -2 , 4, 6,7 ,8{ , B = }-2, 1,4 , 8 ,9{ , C= }-4, -2, 4,7, 9{ تناكاذإ (6( لاثم
ْ ِّ
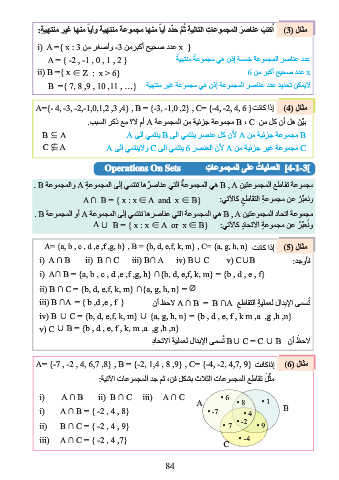
:ةيتلآا تاعومجملا دج مث ،نف لكشب ثلاثلا تاعومجملا عطاقت لثم

i) A ∩ B ii) B ∩ C iii) A ∩ C 6
A 8 1
i) A ∩ B = } -2 , 4 , 8{ -7 4 B

ii) B ∩ C = } -2 , 4 , 9{ 7 -2 9

iii) A ∩ C = } -2 , 4 ,7{ -4
C

84