Page 55 - 수학(하)

예제 01 함수의 뜻

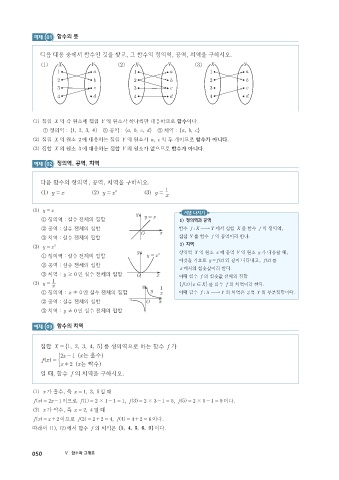
다음 대응 중에서 함수인 것을 찾고, 그 함수의 정의역, 공역, 치역을 구하시오.
Y
Y
1 ]g 2 ]g 3 ]g X Y
X
X
1 a 1 a 1 a
2 b 2 b 2 b
3 c 3 c 3 c
4 d 4 d 4 d

1 ]g 집합 X 의 각 원소에 집합 Y 의 원소가 하나씩만 대응하므로 함수이다.
,
,
,
,
,
,
,
,
"
① 정의역 : 12 34, ② 공역 : ab cd, ③ 치역 : ab c,
"
"
2 ]g 집합 X 의 원소 2 에 대응하는 집합 Y 의 원소가 ,ac 의 두 개이므로 함수가 아니다.
3 ]g 집합 X 의 원소 3 에 대응하는 집합 Y 의 원소가 없으므로 함수가 아니다.
예제 02 정의역, 공역, 치역
다음 함수의 정의역, 공역, 치역을 구하시오.
1
2
1 ]g y = 2 ]g y = x 3 ]g y = x
x
1 ]g y = x
y y = x 개념 다지기
① 정의역 : 실수 전체의 집합 ) 1 정의역과 공역
:
② 공역 : 실수 전체의 집합 함수 fX $ Y 에서 집합 X 를 함수 f 의 정의역,
O x
③ 치역 : 실수 전체의 집합 집합 Y 를 함수 f 의 공역이라 한다.
) 2 치역
2 ]g y = x 2
y 정의역 X 의 원소 x 에 공역 Y 의 원소 y 가 대응할 때,
① 정의역 : 실수 전체의 집합 y = x 2
f x
이것을 기호로 y = ]g 와 같이 나타내고, f x ]g 를
② 공역 : 실수 전체의 집합
x 에서의 함숫값이라 한다.
③ 치역 : y $ 0 인 실수 전체의 집합 O x 이때 함수 f 의 함숫값 전체의 집합
1
3 ]g y = " f x ]g | x ! X, 를 함수 f 의 치역이라 한다.
x y 1
:
① 정의역 : x ! 0 인 실수 전체의 집합 y = x 이때 함수 fX $ Y 의 치역은 공역 Y 의 부분집합이다.
② 공역 : 실수 전체의 집합 O x
③ 치역 : y ! 0 인 실수 전체의 집합
예제 03 함수의 치역

,
,
,
집합 X = " , 12 34 5, 를 정의역으로 하는 함수 f 가
x 2 - 1 ^ x는홀수h
f x = )
] g
x + 2 ^ x는짝수h
일 때, 함수 f 의 치역을 구하시오.
,
1 ]g x 가 홀수, 즉 x = , 13 5 일 때
9
1
f x = x 2 - 이므로 f 1 = 2 # - 1 = 1 , f 3 = 2 # - 1 = 5 , f 5 = 2 # - 1 = 이다.
5
3
1
]g
] g
] g
] g
2 ]g x 가 짝수, 즉 x = , 24 일 때
f x =+ 이므로 f 2 = 2 + 2 = 4 , f 4 = 4 + 2 = 이다.
x
6
2
] g
] g
]g
,
,
,
,
따라서 1 ] g , 2 ] g 에서 함수 f 의 치역은 14 56 9, 이다.
"
050 Ⅴ. 함수와 그래프