Page 58 - 수학(하)

알맹이 콕 !

. 1 일대일함수와 일대일대응
) 1 일대일함수

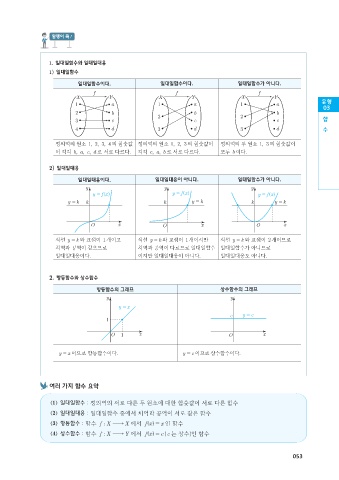
일대일함수이다. 일대일함수이다. 일대일함수가 아니다.
f f f
X Y X Y X Y
1 a 1 a 1 a 유형
03
2 b b b
2 2
3 c c c 함
4 d 3 d 3 d 수

,
,
,
정의역의 원소 ,12 34 의 함숫값 정의역의 원소 ,12 3 의 함숫값이 정의역의 두 원소 ,13 의 함숫값이
,
,
,
이 각각 ,bacd 로 서로 다르다. 각각 ,ca b 로 서로 다르다. 모두 b 이다.
2) 일대일대응
일대일대응이다. 일대일대응이 아니다. 일대일함수가 아니다.
y y y
f x
f x
f x
y = ]g y = ]g y = ]g
y = k k k y = k k y = k

O x O x O x

k
k
k
직선 y = 와 교점이 1개이고 직선 y = 와 교점이 1개이지만 직선 y = 와 교점이 2 개이므로
치역과 공역이 같으므로 치역과 공역이 다르므로 일대일함수 일대일함수가 아니므로
일대일대응이다. 이지만 일대일대응이 아니다. 일대일대응도 아니다.

2. 항등함수와 상수함수

항등함수의 그래프 상수함수의 그래프
y y
y = x
c y = c
1

O 1 x O x

c
x
y = 이므로 항등함수이다. y = 이므로 상수함수이다.

여러 가지 함수 요약

1 ]g 일대일함수 : 정의역의 서로 다른 두 원소에 대한 함숫값이 서로 다른 함수
2 ]g 일대일대응 : 일대일함수 중에서 치역과 공역이 서로 같은 함수
3 ]g 항등함수 : 함수 fX $ X 에서 f x = 인 함수
:
x
]g
4 상수함수 : 함수 fX $
c
]g
]g : Y 에서 f x = ( c 는 상수)인 함수
053