Page 111 - Microeconomics, Fourth Edition

c03consumerpreferencesandtheconceptofutility.qxd 6/14/10 2:54 PM Page 85

3.2 UTILITY FUNCTIONS 85

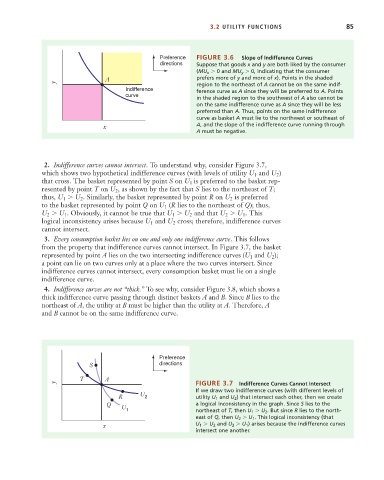
Preference FIGURE 3.6 Slope of Indifference Curves
directions Suppose that goods x and y are both liked by the consumer
(MU x 0 and MU y 0, indicating that the consumer
A prefers more of y and more of x). Points in the shaded
y
region to the northeast of A cannot be on the same indif-
Indifference ference curve as A since they will be preferred to A. Points
curve
in the shaded region to the southwest of A also cannot be
on the same indifference curve as A since they will be less
preferred than A. Thus, points on the same indifference
curve as basket A must lie to the northwest or southeast of
x A, and the slope of the indifference curve running through
A must be negative.

2. Indifference curves cannot intersect. To understand why, consider Figure 3.7,
2
which shows two hypothetical indifference curves (with levels of utility U 1 and U )
that cross. The basket represented by point S on U is preferred to the basket rep-
1
resented by point T on U , as shown by the fact that S lies to the northeast of T;
2
thus, U U . Similarly, the basket represented by point R on U is preferred
2
2
1
to the basket represented by point Q on U (R lies to the northeast of Q); thus,
1
U U . Obviously, it cannot be true that U U and that U U . This
1
2
1
1
2
2
logical inconsistency arises because U and U cross; therefore, indifference curves
2
1
cannot intersect.
3. Every consumption basket lies on one and only one indifference curve. This follows
from the property that indifference curves cannot intersect. In Figure 3.7, the basket
represented by point A lies on the two intersecting indifference curves (U and U );
2
1
a point can lie on two curves only at a place where the two curves intersect. Since
indifference curves cannot intersect, every consumption basket must lie on a single
indifference curve.
4. Indifference curves are not “thick.” To see why, consider Figure 3.8, which shows a
thick indifference curve passing through distinct baskets A and B. Since B lies to the
northeast of A, the utility at B must be higher than the utility at A. Therefore, A
and B cannot be on the same indifference curve.
Preference
S directions
T A
y FIGURE 3.7 Indifference Curves Cannot Intersect
If we draw two indifference curves (with different levels of
R U 2 utility U 1 and U 2 ) that intersect each other, then we create
Q U a logical inconsistency in the graph. Since S lies to the
1 northeast of T, then U 1 U 2 . But since R lies to the north-
east of Q, then U 2 U 1 . This logical inconsistency (that
x U 1 U 2 and U 2 U 1 ) arises because the indifference curves
intersect one another.