Page 563 - Microeconomics, Fourth Edition

c13marketstructureandcompetition.qxd 7/30/10 1:32 PM Page 537

13.2 OLIGOPOLY WITH HOMOGENEOUS PRODUCTS 537

90

S
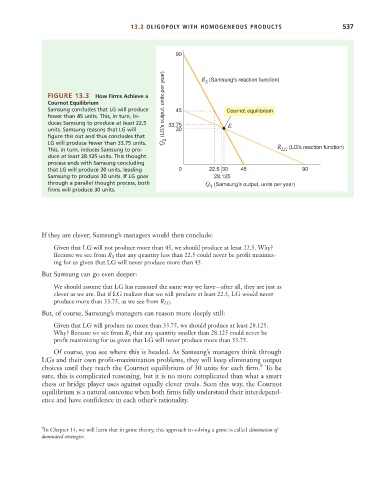
FIGURE 13.3 How Firms Achieve a R (Samsung's reaction function)
Cournot Equilibrium
Samsung concludes that LG will produce Q 2 (LG's output, units per year) 45 Cournot equilibrium
fewer than 45 units. This, in turn, in-
duces Samsung to produce at least 22.5 33.75 E
units. Samsung reasons that LG will 30
figure this out and thus concludes that
LG will produce fewer than 33.75 units. R
This, in turn, induces Samsung to pro- LG (LG's reaction function)
duce at least 28.125 units. This thought
process ends with Samsung concluding
that LG will produce 30 units, leading 0 22.5 30 45 90
Samsung to produce 30 units. If LG goes 28.125
through a parallel thought process, both Q (Samsung's output, units per year)
1
firms will produce 30 units.

If they are clever, Samsung’s managers would then conclude:

Given that LG will not produce more than 45, we should produce at least 22.5. Why?
Because we see from R S that any quantity less than 22.5 could never be profit maximiz-
ing for us given that LG will never produce more than 45.
But Samsung can go even deeper:
We should assume that LG has reasoned the same way we have—after all, they are just as
clever as we are. But if LG realizes that we will produce at least 22.5, LG would never
produce more than 33.75, as we see from R LG .
But, of course, Samsung’s managers can reason more deeply still:

Given that LG will produce no more than 33.75, we should produce at least 28.125.
Why? Because we see from R S that any quantity smaller than 28.125 could never be
profit maximizing for us given that LG will never produce more than 33.75.
Of course, you see where this is headed. As Samsung’s managers think through
LGs and their own profit-maximization problems, they will keep eliminating output
9
choices until they reach the Cournot equilibrium of 30 units for each firm. To be
sure, this is complicated reasoning, but it is no more complicated than what a smart
chess or bridge player uses against equally clever rivals. Seen this way, the Cournot
equilibrium is a natural outcome when both firms fully understand their interdepend-
ence and have confidence in each other’s rationality.

9 In Chapter 14, we will learn that in game theory, this approach to solving a game is called elimination of
dominated strategies.