Page 611 - Microeconomics, Fourth Edition

c14gametheoryandstrategicbehavior.qxd 8/6/10 8:22 AM Page 585

14.2 THE REPEATED PRISONERS’ DILEMMA 585
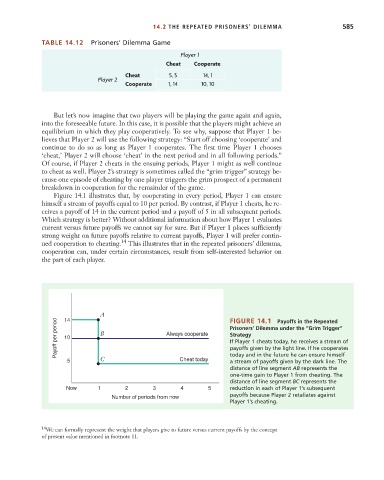
TABLE 14.12 Prisoners’ Dilemma Game

Player 1
Cheat Cooperate
Cheat 5, 5 14, 1
Player 2
Cooperate 1, 14 10, 10

But let’s now imagine that two players will be playing the game again and again,
into the foreseeable future. In this case, it is possible that the players might achieve an
equilibrium in which they play cooperatively. To see why, suppose that Player 1 be-
lieves that Player 2 will use the following strategy: “Start off choosing ‘cooperate’ and
continue to do so as long as Player 1 cooperates. The first time Player 1 chooses
‘cheat,’ Player 2 will choose ‘cheat’ in the next period and in all following periods.”
Of course, if Player 2 cheats in the ensuing periods, Player 1 might as well continue
to cheat as well. Player 2’s strategy is sometimes called the “grim trigger” strategy be-
cause one episode of cheating by one player triggers the grim prospect of a permanent
breakdown in cooperation for the remainder of the game.
Figure 14.1 illustrates that, by cooperating in every period, Player 1 can ensure
himself a stream of payoffs equal to 10 per period. By contrast, if Player 1 cheats, he re-
ceives a payoff of 14 in the current period and a payoff of 5 in all subsequent periods.
Which strategy is better? Without additional information about how Player 1 evaluates
current versus future payoffs we cannot say for sure. But if Player 1 places sufficiently
strong weight on future payoffs relative to current payoffs, Player 1 will prefer contin-
ued cooperation to cheating. 14 This illustrates that in the repeated prisoners’ dilemma,
cooperation can, under certain circumstances, result from self-interested behavior on
the part of each player.

A FIGURE 14.1 Payoffs in the Repeated
14
Payoff per period 10 B Always cooperate Prisoners’ Dilemma under the “Grim Trigger”
Strategy
If Player 1 cheats today, he receives a stream of
payoffs given by the light line. If he cooperates
5 C Cheat today today and in the future he can ensure himself
a stream of payoffs given by the dark line. The
distance of line segment AB represents the
one-time gain to Player 1 from cheating. The
distance of line segment BC represents the
Now 1 2 3 4 5 reduction in each of Player 1’s subsequent
Number of periods from now payoffs because Player 2 retaliates against
Player 1’s cheating.

14 We can formally represent the weight that players give to future versus current payoffs by the concept
of present value mentioned in footnote 11.