Page 116 - Fiber Optic Communications Fund

Lasers 97

× 10 −16
1.6
T = 3000 K
T = 4000 K
1.4 T = 5000 K

1.2

1
u(ω), Arb. unit 0.8

0.6

0.4

0.2

0
0 1 2 3 4 5 6 7 8 9 10
Angular frequency, ω (rad/s) 15
× 10
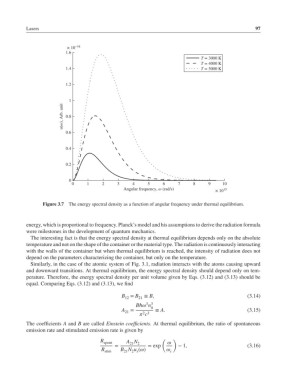
Figure 3.7 The energy spectral density as a function of angular frequency under thermal equilibrium.

energy, which is proportional to frequency. Planck’s model and his assumptions to derive the radiation formula
were milestones in the development of quantum mechanics.
The interesting fact is that the energy spectral density at thermal equilibrium depends only on the absolute
temperature and not on the shape of the container or the material type. The radiation is continuously interacting
with the walls of the container but when thermal equilibrium is reached, the intensity of radiation does not
depend on the parameters characterizing the container, but only on the temperature.
Similarly, in the case of the atomic system of Fig. 3.1, radiation interacts with the atoms causing upward
and downward transitions. At thermal equilibrium, the energy spectral density should depend only on tem-
perature. Therefore, the energy spectral density per unit volume given by Eqs. (3.12) and (3.13) should be
equal. Comparing Eqs. (3.12) and (3.13), we find

B = B ≡ B, (3.14)
12 21
3 3
Bℏ n 0
A = ≡ A. (3.15)
21
c
2 3
The coefficients A and B are called Einstein coefficients. At thermal equilibrium, the ratio of spontaneous
emission rate and stimulated emission rate is given by
R ( )
spont A N
21 2
= = exp − 1, (3.16)
R B N u ()
stim 21 2 s c