Page 285 - Fiber Optic Communications Fund

266 Fiber Optic Communications

gain occurs when the signal frequency is equal to one of the resonant frequencies given by Eq. (6.126), and
it is given by
(1 − R )(1 − R )G (f)
s
2
1
G = . (6.127)
peak 2
(1 − RG )
s
The separation between two peaks is known as the free spectral range (FSR):
c
FSR = f m+1 − f = . (6.128)
m
2nL
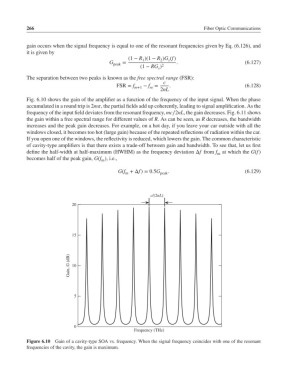
Fig. 6.10 shows the gain of the amplifier as a function of the frequency of the input signal. When the phase
accumulated in a round trip is 2m, the partial fields add up coherently, leading to signal amplification. As the
frequency of the input field deviates from the resonant frequency, mc∕2nL, the gain decreases. Fig. 6.11 shows
the gain within a free spectral range for different values of R. As can be seen, as R decreases, the bandwidth
increases and the peak gain decreases. For example, on a hot day, if you leave your car outside with all the
windows closed, it becomes too hot (large gain) because of the repeated reflections of radiation within the car.
If you open one of the windows, the reflectivity is reduced, which lowers the gain. The common characteristic
of cavity-type amplifiers is that there exists a trade-off between gain and bandwidth. To see that, let us first
define the half-width at half-maximum (HWHM) as the frequency deviation Δf from f at which the G(f)
m
becomes half of the peak gain, G(f ), i.e.,
m
G(f +Δf)= 0.5G . (6.129)
m peak

c/(2nL)
20

15

Gain, G (dB) 10

5

0
Frequency (THz)

Figure 6.10 Gain of a cavity-type SOA vs. frequency. When the signal frequency coincides with one of the resonant
frequencies of the cavity, the gain is maximum.