Page 286 - Fiber Optic Communications Fund

Optical Amplifiers 267

20
18

R = 0.3
16
14

Gain, G (dB) 12 8
10

6
4 R = 0.1

2
0
1.935 1.935 1.935 1.935 1.935 1.935 1.935
Frequency (THz) × 10 4

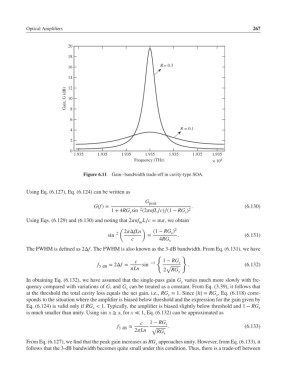
Figure 6.11 Gain–bandwidth trade-off in cavity-type SOA.

Using Eq. (6.127), Eq. (6.124) can be written as
G peak
G(f)= . (6.130)
2
1 + 4RG sin (2nfL∕c)∕(1 − RG ) 2
s
s
Using Eqs. (6.129) and (6.130) and noting that 2nf L∕c = m, we obtain
m
( ) 2
2ΔfLn (1 − RG )
s
2
sin = . (6.131)
c 4RG
s
The FWHM is defined as 2Δf. The FWHM is also known as the 3-dB bandwidth. From Eq. (6.131), we have
{ }
c −1 1 − RG s
f = 2Δf = sin . (6.132)
3dB √
Ln 2 RG s
In obtaining Eq. (6.132), we have assumed that the single-pass gain G varies much more slowly with fre-
s
quency compared with variations of G, and G can be treated as a constant. From Eq. (3.39), it follows that
s
at the threshold the total cavity loss equals the net gain, i.e., RG = 1. Since |h| = RG , Eq. (6.118) corre-
s
s
sponds to the situation where the amplifier is biased below threshold and the expression for the gain given by
Eq. (6.124) is valid only if RG < 1. Typically, the amplifier is biased slightly below threshold and 1 − RG s
s
is much smaller than unity. Using sin x ≅ x,for x ≪ 1, Eq. (6.132) can be approximated as
c 1 − RG s
f 3dB ≈ √ . (6.133)
2Ln RG
s
From Eq. (6.127), we find that the peak gain increases as RG approaches unity. However, from Eq. (6.133), it
s
follows that the 3-dB bandwidth becomes quite small under this condition. Thus, there is a trade-off between