Page 43 - Fiber Optic Communications Fund

24 Fiber Optic Communications

B
E

ϕ 2
n 2
G
C x
ϕ 1
y
n 1
A D F
x
Figure 1.21 Refraction of a light wave.

Therefore, Eq. (1.144) becomes
n sin = n sin . (1.146)
1 1 2 2
This is called Snell’s law.If n > n ,sin > sin and > . This explains why light bends toward the
1
2
1
2
1
2
normal in a denser medium, as shown in Fig. 1.18.
When n > n , from Eq. (1.146), we have > . As the angle of incidence increases, the angle of
1
1
2
1
2
refraction increases too. For a particular angle, = , becomes ∕2,
1
2
c
2
n sin = n sin ∕2 (1.147)
1
2
c
or
sin = n ∕n . (1.148)
c 2 1
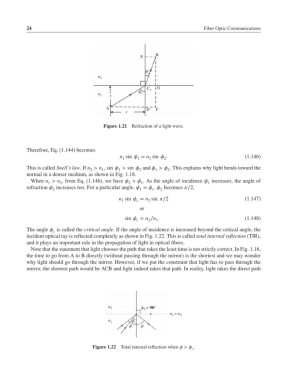
The angle is called the critical angle. If the angle of incidence is increased beyond the critical angle, the
c
incident optical ray is reflected completely as shown in Fig. 1.22. This is called total internal reflection (TIR),
and it plays an important role in the propagation of light in optical fibers.
Note that the statement that light chooses the path that takes the least time is not strictly correct. In Fig. 1.16,
the time to go from A to B directly (without passing through the mirror) is the shortest and we may wonder
why light should go through the mirror. However, if we put the constraint that light has to pass through the
mirror, the shortest path would be ACB and light indeed takes that path. In reality, light takes the direct path
n 2 ϕ 2 = 90°
n 1 > n 2
n 1 ϕ c
ϕ ϕ

Figure 1.22 Total internal reflection when > .
c