Page 40 - Fiber Optic Communications Fund

Electromagnetics and Optics 21

x
k

k x
30°
z
k z
∘
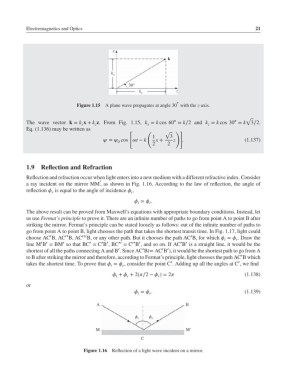
Figure 1.15 A plane wave propagates at angle 30 with the z-axis.

∘ ∘ √
The wave vector k = k x + k z.FromFig.1.15, k = k cos 60 = k∕2 and k = k cos 30 = k 3∕2.
x
x
z
z
Eq. (1.136) may be written as
[ ( √ )]
1 3
= cos t − k x + z . (1.137)
0
2 2
1.9 Reflection and Refraction
Reflection and refraction occur when light enters into a new medium with a different refractive index. Consider
′
a ray incident on the mirror MM, as shown in Fig. 1.16. According to the law of reflection, the angle of
reflection is equal to the angle of incidence ,
r i
= .
i
r
The above result can be proved from Maxwell’s equations with appropriate boundary conditions. Instead, let
us use Fermat’s principle to prove it. There are an infinite number of paths to go from point A to point B after
striking the mirror. Fermat’s principle can be stated loosely as follows: out of the infinite number of paths to
go from point A to point B, light chooses the path that takes the shortest transit time. In Fig. 1.17, light could
′
′′
′′′
′
choose AC B, AC B, AC B, or any other path. But it chooses the path AC B, for which = .Drawthe
i r
′′ ′
′ ′
′
′ ′
′ ′
′′
′
line M B = BM so that BC = C B ,BC = C B , and so on. If AC B is a straight line, it would be the
′ ′
′
′
shortest of all the paths connecting A and B . Since AC B(= AC B ), it would be the shortest path to go from A
′
to B after striking the mirror and therefore, according to Fermat’s principle, light chooses the path AC B which
′
′
takes the shortest time. To prove that = , consider the point C . Adding up all the angles at C , we find
i
r
+ + 2(∕2 − )= 2 (1.138)
r
i
r
or
= . (1.139)
i r
A B
ϕ i ϕ r
M Mʹ
C
Figure 1.16 Reflection of a light wave incident on a mirror.