Page 86 - Fiber Optic Communications Fund

Optical Fiber Transmission 67

where is the instantaneous phase of the field envelope and (t) is the instantaneous frequency deviation
from the carrier frequency. Note that the optical carrier is of the form exp (−i t). A negative sign is introduced
0
above so that a positive value of implies the frequency is up-shifted. At the fiber output, from Eq. (2.160),
the instantaneous phase is
2
t L
2
(t)=− 2 2 + const. (2.166)
2T T
1 0
Substituting Eq. (2.166) in Eq. (2.165), we find
( )
L
2
(t)= 2 2 t. (2.167)
T T
1 0
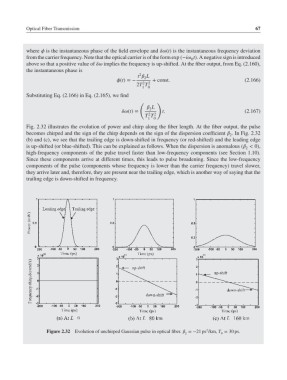
Fig. 2.32 illustrates the evolution of power and chirp along the fiber length. At the fiber output, the pulse
becomes chirped and the sign of the chirp depends on the sign of the dispersion coefficient . In Fig. 2.32
2
(b) and (c), we see that the trailing edge is down-shifted in frequency (or red-shifted) and the leading edge
is up-shifted (or blue-shifted). This can be explained as follows. When the dispersion is anomalous ( < 0),
2
high-frequency components of the pulse travel faster than low-frequency components (see Section 1.10).
Since these components arrive at different times, this leads to pulse broadening. Since the low-frequency
components of the pulse (components whose frequency is lower than the carrier frequency) travel slower,
they arrive later and, therefore, they are present near the trailing edge, which is another way of saying that the
trailing edge is down-shifted in frequency.

2
Figure 2.32 Evolution of unchirped Gaussian pulse in optical fiber. =−21 ps /km, T = 30 ps.
2
0