Page 284 - Services Selection Board (SSB) Interviews

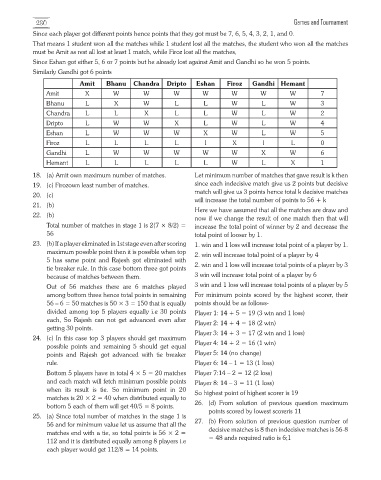
280 Games and Tournament
Since each player got different points hence points that they got must be 7, 6, 5, 4, 3, 2, 1, and 0.
That means 1 student won all the matches while 1 student lost all the matches, the student who won all the matches
must be Amit as rest all lost at least 1 match, while Firoz lost all the matches,
Since Eshan got either 5, 6 or 7 points but he already lost against Amit and Gandhi so he won 5 points.
Similarly Gandhi got 6 points
Amit Bhanu Chandra Dripto Eshan Firoz Gandhi Hemant
Amit X W W W W W W W 7
Bhanu L X W L L W L W 3
Chandra L L X L L W L W 2

Dripto L W W X L W L W 4
Eshan L W W W X W L W 5
Firoz L L L L l X l L 0
Gandhi L W W W W W X W 6
Hemant L L L L L W L X 1
18. (a) Amit own maximum number of matches. Let minimum number of matches that gave result is k then
19. (c) Firozown least number of matches. since each indecisive match give us 2 points but decisive
20. (c) match will give us 3 points hence total k decisive matches
will increase the total number of points to 56 + k
21. (b) Here we have assumed that all the matches are draw and
22. (b) now if we change the result of one match then that will
Total number of matches in stage 1 is 2(7 × 8/2) = increase the total point of winner by 2 and decrease the
56 total point of looser by 1.
23. (b) If a player eliminated in 1st stage even after scoring 1. win and 1 loss will increase total point of a player by 1.
maximum possible point then it is possible when top 2. win will increase total point of a player by 4
5 has same point and Rajesh got eliminated with
tie breaker rule. In this case bottom three got points 2. win and 1 loss will increase total points of a player by 3
because of matches between them. 3 win will increase total point of a player by 6
Out of 56 matches there are 6 matches played 3 win and 1 loss will increase total points of a player by 5
among bottom three hence total points in remaining For minimum points scored by the highest scorer, their
56 – 6 = 50 matches is 50 × 3 = 150 that is equally points should be as follows-
divided among top 5 players equally i.e 30 points Player 1: 14 + 5 = 19 (3 win and 1 loss)
each, So Rajesh can not get advanced even after Player 2: 14 + 4 = 18 (2 win)
getting 30 points.
24. (c) In this case top 3 players should get maximum Player 3: 14 + 3 = 17 (2 win and 1 loss)
possible points and remaining 5 should get equal Player 4: 14 + 2 = 16 (1 win)
points and Rajesh got advanced with tie breaker Player 5: 14 (no change)
rule. Player 6: 14 – 1 = 13 (1 loss)
Bottom 5 players have in total 4 × 5 = 20 matches Player 7:14 – 2 = 12 (2 loss)
and each match will fetch minimum possible points Player 8: 14 – 3 = 11 (1 loss)
when its result is tie. So minimum point in 20 So highest point of highest scorer is 19
matches is 20 × 2 = 40 when distributed equally to
bottom 5 each of them will get 40/5 = 8 points. 26. (d) From solution of previous question maximum
25. (a) Since total number of matches in the stage 1 is points scored by lowest scoreris 11
56 and for minimum value let us assume that all the 27. (b) From solution of previous question number of
matches end with a tie, so total points is 56 × 2 = decisive matches is 8 then indecisive matches is 56-8
112 and it is distributed equally among 8 players i.e = 48 ands required ratio is 6;1
each player would get 112/8 = 14 points.