Page 18 - Gerak Satu Dimensi-Blog Pembelajaran Fisika Dasar-FKIP Untad

Menentukan Kecepatan dan Posisi dengan Integrasi

c. sketsa grafik − , − , dan −

Jawab:
1
a. − = +
2

2
1
− 0 = 0. +
2
2
1
= . 9,8. 2,5
2
2
= 30,624
Jadi tinggi bangunan tersebut adalah 30,624
b. = + = 0 + 9,8.2,5 = 24,5 /

Jadi Kecepatan batu bata sesaat sebelum mencapai permukaan tanah sebesar 24,5 /
c.

H. Menentukan Kecepatan dan Posisi dengan Integrasi
Banyak keadaan fisika yang posisi dan kecepatan tidak diketahui sebagai fungsi
waktu, tetapi hanya diketahu percepatan. Posisi dan kecepatan dapat dicari dari fungsi

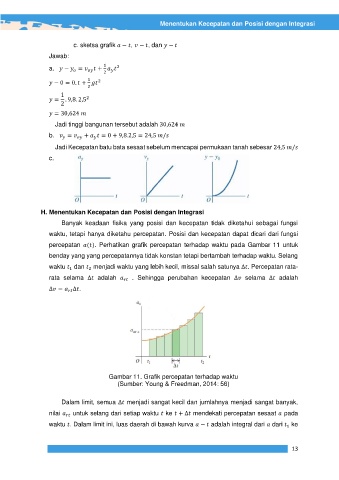
percepatan ( ). Perhatikan grafik percepatan terhadap waktu pada Gambar 11 untuk
benday yang yang percepatannya tidak konstan tetapi bertambah terhadap waktu. Selang

waktu dan menjadi waktu yang lebih kecil, missal salah satunya ∆ . Percepatan rata-
2
1
rata selama ∆ adalah . Sehingga perubahan kecepatan ∆ selama ∆ adalah

∆ = ∆ .

Gambar 11. Grafik percepatan terhadap waktu
(Sumber: Young & Freedman, 2014: 56)

Dalam limit, semua ∆ menjadi sangat kecil dan jumlahnya menjadi sangat banyak,

nilai untuk selang dari setiap waktu ke + ∆ mendekati percepatan sesaat pada

waktu . Dalam limit ini, luas daerah di bawah kurva − adalah integral dari dari ke
1

13