Page 36 - E-Book Matematika Pythagoras
P. 36
Rangkuman
bahwa kuadrat panjang sisi miring segitiga siku-siku
1. Teorema Pythagoras menyatakan
a
h kua
si
t si
dra
ada Jadi, jarak mendaratnya adalah 1,44 km. i lainnya.
ma d
lah sa
nga
e
n jum
l
-
sis
2. Teorema Pythagoras ditulis sebagai berikut :
• = +
• = + atau, = √ +
• = − atau, = √ −
• = − atau = √ −
•
3. Dalam ∆ berlaku kebalikan teorema Pythagoras, yaitu:
Jika = + ,maka ∆ siku-siku di A.
Jika = + ,maka ∆ siku-siku di B.
Jika = + ,maka ∆ siku-siku di C.
4. Untuk ∆ dengan panjang sisi-sisinya , , dan :
2
2
2
a. Jika < + , maka ∆ merupakan segitiga lancip di . Sisi dihadapkan sudut
dan merupakan sisi terpanjang.
2
2
2
b. Jika > + , maka ∆ merupakan segitiga tumpul di . Sisi terletak dihadapan
sudut dan merupakan sisi terpanjang.
5. Tripel (tigaan) pythagoras adalah tigaan bilangan asli yang tepat untuk menyatakan panjang
sisi-sisi suatu segitiga siku-siku.
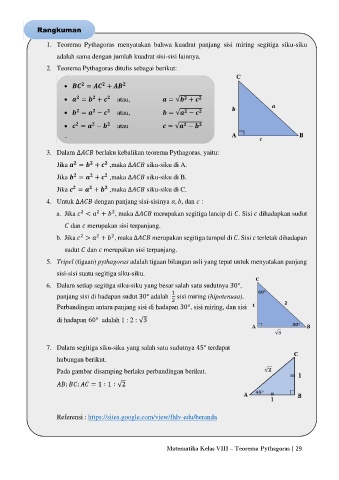
6. Dalam setiap segitiga siku-siku yang besar salah satu sudutnya 30°,
1
panjang sisi di hadapan sudut 30° adalah sisi miring (hipotenusa).
2
Perbandingan antara panjang sisi di hadapan 30°, sisi miring, dan sisi
di hadapan 60° adalah 1 : 2 : √3
7. Dalam segitiga siku-siku yang salah satu sudutnya 45° terdapat
hubungan berikut.
Pada gambar disamping berlaku perbandingan berikut.
: : = 1 ∶ 1 ∶ √2
Referensi : https://sites.google.com/view/fhlv-edu/beranda
Matematika Kelas VIII – Teorema Pythagoras | 29