Page 9 - Cálculo Integral: Guía I

INSTITUTO POLITÉCNICO NACIONAL
CECYT “WILFRIDO MASSIEU”
Unidades de Aprendizaje del Área Básica

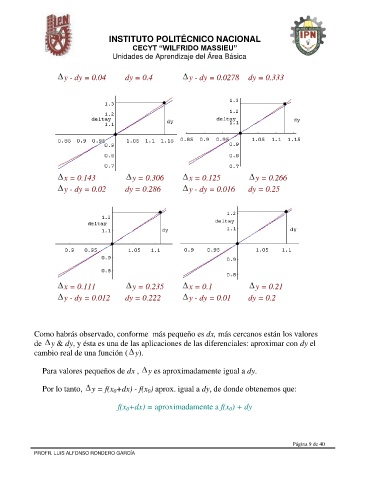
y - dy = 0.04 dy = 0.4 y - dy = 0.0278 dy = 0.333

x = 0.143 y = 0.306 x = 0.125 y = 0.266
y - dy = 0.02 dy = 0.286 y - dy = 0.016 dy = 0.25

x = 0.111 y = 0.235 x = 0.1 y = 0.21

y - dy = 0.012 dy = 0.222 y - dy = 0.01 dy = 0.2

Como habrás observado, conforme más pequeño es dx, más cercanos están los valores
de y & dy, y ésta es una de las aplicaciones de las diferenciales: aproximar con dy el
cambio real de una función ( y).

Para valores pequeños de dx , y es aproximadamente igual a dy.

Por lo tanto, y = f(x +dx) - f(x ) aprox. igual a dy, de donde obtenemos que:
0
0
f(x +dx) = aproximadamente a f(x ) + dy
0
0

Página 9 de 40
PROFR. LUIS ALFONSO RONDERO GARCÍA