Page 315 - FUNDAMENTALS OF COMPUTER

NPP Number System, Boolean Algebra and Logic Circuits 315

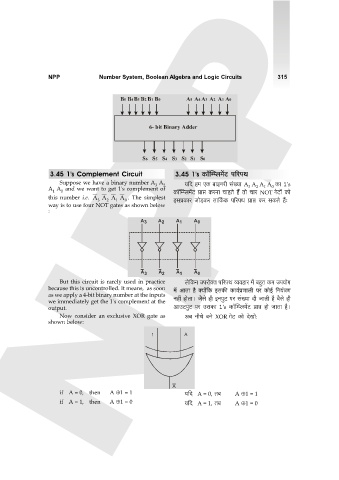
B5 B4 B3 B2 B1 B0 A5 A4 A3 A2 A1 A0

6- bit Binary Adder

S6 S5 S4 S3 S2 S1 S0

3.45 1's Complement Circuit 3.45 1's H$m°påßb_|Q> n[anW
Suppose we have a binary number A A `{X h_ EH$ ~mBZar g§»`m A A A A H$m 1's
3
3
0
1
2
A A and we want to get 1's complement of 2 H$m°påßb_|Q> àmá H$aZm MmhVo h¢ Vmo Mma NOT JoQ>m| H$mo
0
1
this number i.e. A 3 A 2 A 1 A . The simplest BgàH$ma Omo‹S>H$a Vm{H©$H$ n[anW àmá H$a gH$Vo h¢…
0
way is to use four NOT gates as shown below
: NPP
A 3 A 2 A 1 A 0

A 3 A 2 A 1 A 0
But this circuit is rarely used in practice bo{H$Z CnamoŠV n[anW ì`dhma _| ~hþV H$_ Cn`moJ
because this is uncontrolled. It means, as soon _| AmVm h¡ Š`m|{H$ BgH$s H$m`©àUmbr na H$moB© {Z`§ÌU
as we apply a 4-bit binary number at the inputs
we immediately get the 1's complement at the Zht hmoVmŸ& O¡go hr BZnwQ> na g§»`m Xr OmVr h¡ d¡go hr
output. AmCQ>nwQ> na CgH$m 1's H$m°påßb_|Q> àmá hmo OmVm h¡Ÿ&
Now consider an exclusive XOR gate as A~ ZrMo ~Zo XOR JoQ> H$mo XoImo:
shown below:

1 A

A
if A = 0, then A ⊕1 = 1 `{X A = 0, V~ A ⊕1 = 1
if A = 1, then A ⊕1 = 0 `{X A = 1, V~ A ⊕1 = 0