Page 130 - analysinew

130
ΚΕΦΑΛΑΙΟ 1 - Όρια - Συνέχεια Συνάρτησης

ΜΟΡΦΗ : f(g(x))+f(h(x))=...
ΖΗΤΟΥΜΕΝΟ : ο τύπος ή τιμή της συναρτησης f

AΝΤΙΜΕΤΩΠΙΣΗ
● Θέτουμε x = g(x), ώστε η f(g(x)) να μετατραπεί σε f(x),
ενώ η f(h(x)) θα μετατραπεί, έστω σε f(r(x)).
[Έχουμε εξίσωση ως προς f(x), f(r(x)) (1)].
● Θέτουμε x = r(x) και προκύπτει νέα σχέση με f(r(x)) και
f(x) (2)
● Απαλείφουμε το f(r(x)) στις (1) και (2) και έχουμε το τύπο
της f ...
● Στη περίπτωση εύρεσης κάποιας τιμής της συνάρτησης,
στον τύπο της, που β ρ ήκαμε, αντικαθιστούμε τον x με την
συγκεκριμένη τιμή .

ΠΑΡΑΔΕΙΓΜΑ
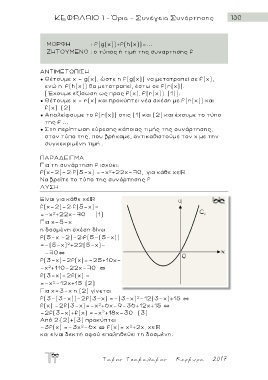
Για τη συνάρτηση f ισχύει:
f(x-2)-2 f(5-x) =-χ +22x-70, για κάθε χ

2
Να βρείτε το τύπο της συνάρτησης f
ΛΥΣ Η

Είναι για κάθε χ
f(x-2)-2 f(5-x)=
=-χ +22x-70 (1)
2
Για x=5-x

η δοσμένη σχέση δίνει
f(5-x -2)-2 f(5-(5-x))=
=-(5-x) +22(5-x)-
2
-70`
f(3-x)-2f(x)=-25+10x-
2
-x +110-22x-70 `
f(3-x)-2f(x) =

2

=-x -12x+15 (2)

Για x=3-x η (2) γίνεται
2
f(3-(3-x))-2f(3-x) =-(3-x) -12(3-x)+15 `
f(x) -2f(3-x)=-χ +6x-9-36+12χ+15 `
2
-2f(3-x)+f(x) =-χ +18x-30 (3)
2
Από 2 (2)+(3) προκύπτει
-3f(x) =-3x -6x ` f(x)= x +2x, χ
2
2
και είναι δεκτή αφού επαληθεύει τη δοσμένη.

Τακης Τσακαλακος Κερκυρα 2017