Page 126 - olokliroma

126
ΚΕΦΑΛΑΙΟ 3 - Ολοκληρωτικός Λογισμός

● Αν έχουμε δύο δοσμένα σημεία του άξονα χ’χ και τη τε-
τμημένη (ες) των σημείων τομής των C f και C g , τότε
βρίσκουμε το εμβαδόν σε καθένα α π ό τα διαστήματα που
δημιουργούνται από τα δοσμένα σημεία και τη τετμημένη
(ες) των σημείων τομής των C f και C g

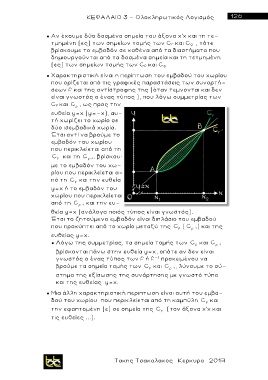
● Χαρακτηριστική είναι η περίπτωση του εμβαδού του χωρίου
που ορίζεται από τις γραφικές παραστάσεις των συναρτή-
σεων f και της αντίστροφης της (όταν τεμνονται και δεν
είναι γνωστός ο ένας τύπος ), που λόγω συμμετρίας των
C f και C 1 ως προς την
f
ευθεία y=x (y=-x), αυ-
τή χωρίζει το χωρίο σε
δύο ισεμβαδικά χωρία.
Έτσι αντί να βρούμε το
εμβαδόν του χωρίου
που περικλείεται από τη
C και τη C f 1 , βρίσκου-
f
με το εμβαδόν του χ ω -
ρίου που περικλείεται α-
π ό τη C και την ευθεία
f
y=χ ή το εμβαδόν του
χωρίου που περικλείεται
από τη C 1 και την ευ-
f
θ ε ία y=χ (ανάλογα ποιός τύπος είναι γνωστός ) .
Έτσι το ζητούμενο εμβαδόν είναι δ ι πλάσιο του εμβαδού
που προκύπτει α π ό το χωρίο μεταξύ της C ( C f 1 ) και της
f
ευθείας y=χ.
● Λόγω της συμμετρίας, τα σημεία τομής των C και C f 1
f
β ρ ίσκονται πάνω στην ευθεία y=χ, οπότε αν δεν είναι
γνωστός ο ένας τύπος των f ή f - 1 προκειμένου να
βρούμε τα σημεία τομής των C και C f 1 , λύνουμε το σύ-
f
στημα της εξίσωσης της συνάρτησης με γνωστό τύπο
και της ευθείας y=χ.

● Μια άλλη χαρακτηριστική περιπτωση είναι αυτή του εμβα-
δ ο ύ του χωρίου που περικλείεται από τη καμπύλη C και
f
την εφαπτομένη (ε) σε σημείο της C (τον άξονα χ’χ και
f
τις ευθείες ...).

Τακης Τσακαλακος Κερκυρα 2017