Page 123 - olokliroma

123
ΚΕΦΑΛΑΙΟ 3 - Ολοκληρωτικός Λογισμός

Π α ρ α τ η ρ ή σ ε ι ς

● Ένα από τα παραπάνω σημεία μπορεί να είναι το χ=0
(άξονας y’y)

● Αν έχουμε δύο δοσμένα σημεία του άξονα χ’χ και ρίζα (ες)
της εξίσωσης της συνάρτησης f, τότε βρίσκουμε το εμ-
βαδόν σε καθένα από τα διαστήματα που δημιουργούνται
από τα δοσμένα σημεία και τη ρίζα (ες) της εξίσωσης της
συνάρτησης f

● Χαρακτηριστική είναι η περίπτωση της αντίστροφης συν-
άρτησης της f
(όταν δεν είναι γνωστός ο τύπος της), που λόγω συμμε-
τ ρ ίας των C f και C 1 ως προς τη ευθεία y=x (y=-x), αντί
f
να βρούμε το εμβαδόν του χωρίου που περικλείεται από τη
C 1 τον χ’χ και τις ευθείες χ=α, χ=β, βρίσκουμε το εμβα-
f
δόν χωρίου που περικλείεται από τη C τον y’y και τις ευ-
f
θείες y=α, χ=β.
Το επιτυγχάνουμε με
δύο τ ρ όπους
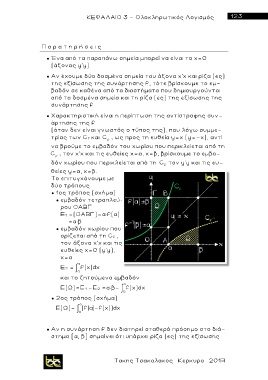
● 1ος τρόπος (σχήμα)
● εμβαδόν τετραπλεύ-
ρου ΟΑΒΓ
E 1 =(ΟΑΒΓ)=α×f(α)
= α ×β
● εμβαδόν χωρίου που
ορίζεται α π ό τη C f ,
τον άξονα χ’χ και τις
ευθείες χ=0 (y’y),
χ=α
α
E 2 = f(x)dx
0
και το ζητούμενο εμβαδόν
α
Ε(Ω)=E 1 -E 2 = α ×β- f(x)dx
0
● 2ος τρόπος (σχήμα )
α
Ε(Ω)= (f( )-f(x))dx
0

● Αν η συνάρτηση f δεν διατηρεί σταθερό πρόσημο στο διά-
στημα [α, β] σημαίνει ότι υπάρχει ρίζα (ες) της εξίσωσης

Τακης Τσακαλακος Κερκυρα 2017