Page 125 - olokliroma

125
ΚΕΦΑΛΑΙΟ 3 - Ολοκληρωτικός Λογισμός

ΕΜΒΑΔΟΝ ΧΩΡΊΟΥ Ω (ΔΥΟ ΣΥΝΑΡΤΗΣΕΙΣ)

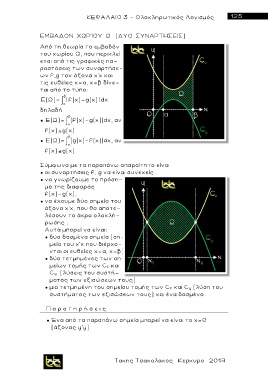
Από τη θεωρία το εμβαδόν
του χωρίου Ω, που περικλεί-
εται από τι ς γραφικές πα-
ραστάσεις τω ν συναρτήσε-
ω ν f,g τον άξονα χ’χ και
τις ευθείες χ=α, χ=β δίνε-
ται από το τύπο:
β
Ε(Ω)= | f(x)-g(x)| dx
α
δηλαδή
β
● Ε(Ω)= (f(x)-g(x))dx, αν
α
f(x) g(x)
β
● Ε(Ω)= (g(x)-f(x))dx, αν
α
f(x) g(x)

Σύμφωνα με τα παραπάνω απαραίτητο είναι
● oι συναρτήσεις f, g να είναι συνεχείς .
● να γνωρίζουμε το πρόση-
μ ο της διαφοράς
f(x)-g(x).
● να έχουμε δύο σημεία του
άξονα χ’χ, που θα α π οτ ε -
λέσουν τα άκρα ολοκλή-
ρωσης .
Αυτά μπορεί να είναι:
● δύο δοσμένα σημεία (ση-
μεία του χ’χ που διέρχο-
νται οι ευθείες χ=α, χ=β)
● δύο τετμημένες των σ η -
μ ε ίων τομής τω ν C f και
C g (λύσεις του συστή-
ματος των εξισώσεων τους )
● μια τετμημένη του σημείου τομής των C f και C g (λύσ η του
συστήματος των εξισώσεων τους) και ένα δοσμένο

Π α ρ α τ η ρ ή σ ε ι ς

● Ένα από τα παραπάνω σημεία μπορεί να είναι το χ=0
(άξονας y’y)

Τακης Τσακαλακος Κερκυρα 2017