Page 59 - E-MODUL_TRANSFORMASI GEOMETRI_KELAS XI
P. 59
Transformasi Geometri Matematika untuk SMA/MA Kelas XI 55
2
3 Investigation
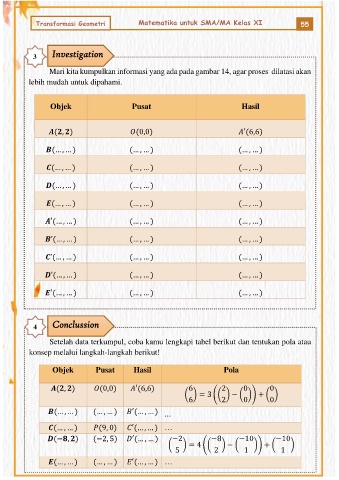
Mari kita kumpulkan informasi yang ada pada gambar 14, agar proses dilatasi akan
lebih mudah untuk dipahami.
Objek Pusat Hasil
( , ) (0,0) ′(6,6)
(… , … ) (… , … ) (… , … )
(… , … ) (… , … ) (… , … )
(… , … ) (… , … ) (… , … )
(… , … ) (… , … ) (… , … )
′(… , … ) (… , … ) (… , … )
’(… , … ) (… , … ) (… , … )
’(… , … ) (… , … ) (… , … )
’(… , … ) (… , … ) (… , … )
′(… , … ) (… , … ) (… , … )
4 Conclussion
Setelah data terkumpul, coba kamu lengkapi tabel berikut dan tentukan pola atau
konsep melalui langkah-langkah berikut!
Objek Pusat Hasil Pola
( , ) (0,0) ′(6,6) 6 2 0 0
൬ ൰ = 3 ቆ൬ ൰ − ൬ ൰ቇ + ൬ ൰
6 2 0 0
(… , … ) (… , … ) ′(… , … ) …
(… , … ) (9, 0) ′(… , … ) …
(− , ) (−2, 5) ′(… , … ) −2 −8 −10 −10
൬ ൰ = 4 ቆ൬ ൰ − ൬ ൰ቇ + ൬ ൰
5 2 1 1
(… , … ) (… , … ) ′(… , … ) …