Page 335 - Six Sigma Advanced Tools for Black Belts and Master Black Belts

OTE/SPH
OTE/SPH
Char Count= 0
3:6
JWBK119-20
August 31, 2006
320 A Unified Approach for Dual Response Surface Optimization
T
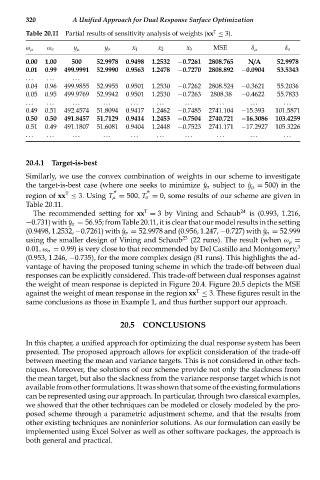
Table 20.11 Partial results of sensitivity analysis of weights (xx ≤ 3).
MSE
ω μ ω σ y μ y σ x 1 x 2 x 3 δ μ δ σ
0.00 1.00 500 52.9978 0.9498 1.2532 −0.7261 2808.765 N/A 52.9978
0.01 0.99 499.9991 52.9990 0.9563 1.2478 −0.7270 2808.892 −0.0904 53.5343
... ... ...
0.04 0.96 499.9855 52.9955 0.9501 1.2530 −0.7262 2808.524 −0.3621 55.2036
0.05 0.95 499.9769 52.9942 0.9501 1.2530 −0.7263 2808.38 −0.4622 55.7833
... ... ... ... ... ... ... ... ... ...
0.49 0.51 492.4574 51.8094 0.9417 1.2462 −0.7485 2741.104 −15.393 101.5871
0.50 0.50 491.8457 51.7129 0.9414 1.2453 −0.7504 2740.721 −16.3086 103.4259
0.51 0.49 491.1807 51.6081 0.9404 1.2448 −0.7523 2741.171 −17.2927 105.3226
... ... ... ... ... ... ... ... ... ...

20.4.1 Target-is-best
Similarly, we use the convex combination of weights in our scheme to investigate
the target-is-best case (where one seeks to minimize ˆy σ subject to ˆy μ = 500) in the
*
*
T
region of xx ≤ 3. Using T μ = 500, T σ = 0, some results of our scheme are given in
Table 20.11.
T
The recommended setting for xx = 3 by Vining and Schaub 24 is (0.993, 1.216,
−0.731) with ˆy σ = 56.95; from Table 20.11, it is clear that our model results in the setting
(0.9498, 1.2532, −0.7261) with ˆy σ = 52.9978 and (0.956, 1.247, −0.727) with ˆy σ = 52.999
using the smaller design of Vining and Schaub 23 (22 runs). The result (when ω μ =
0.01,ω σ = 0.99) is very close to that recommended by Del Castillo and Montgomery, 3
(0.953, 1.246, −0.735), for the more complex design (81 runs). This highlights the ad-
vantage of having the proposed tuning scheme in which the trade-off between dual
responses can be explicitly considered. This trade-off between dual responses against
the weight of mean response is depicted in Figure 20.4. Figure 20.5 depicts the MSE
T
against the weight of mean response in the region xx ≤ 3. These figures result in the
same conclusions as those in Example 1, and thus further support our approach.

20.5 CONCLUSIONS

In this chapter, a unified approach for optimizing the dual response system has been
presented. The proposed approach allows for explicit consideration of the trade-off
between meeting the mean and variance targets. This is not considered in other tech-
niques. Moreover, the solutions of our scheme provide not only the slackness from
the mean target, but also the slackness from the variance response target which is not
available from other formulations. It was shown that some of the existing formulations
can be represented using our approach. In particular, through two classical examples,
we showed that the other techniques can be modeled or closely modeled by the pro-
posed scheme through a parametric adjustment scheme, and that the results from
other existing techniques are noninferior solutions. As our formulation can easily be
implemented using Excel Solver as well as other software packages, the approach is
both general and practical.