Page 193 - Maxwell House

SOLUTION OF BASIC EQUATIONS OF ELECTRODYNAMICS 173

For example, we can look for the solutions that satisfy the initial conditions (called Cauchy
conditions) at the moment = 0

(́, 0) = (́)

(́,) � (4.39)
� = (́)
=0
Early we have demonstrated that the vector potential is closely related to the distribution of
energy accumulated in the EM fields. Here and then, the first equity in (4.39) means that we
have at our disposal some initial portion of energy that can be transferred later (i.e. t > 0) into
the process described by (4.38). Evidently, any EM field cannot be generated without such
initial energy injection. Then the bottom identity in (4.39) tells us how fast we deliver this
energy. Omitting the details let compose the solution (4.35) satisficing (4.39) in the form

1 1 +́ ′ ′
(́, ) = ( ( − ́) + ( + ́)) + ∫ ( ) (4.40)

2 2 −́
We offer the reader to verify this solution just putting
(4.40) into (4.35).
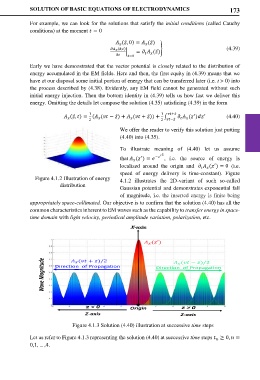
To illustrate meaning of (4.40) let us assume
2
′
′
that ( ) = − , i.e. the source of energy is

localized around the origin and ( ) = 0 (i.e.
′

speed of energy delivery is time-constant). Figure
Figure 4.1.2 Illustration of energy 4.1.2 illustrates the 2D-variant of such so-called
distribution
Gaussian potential and demonstrates exponential fall
of magnitude, i.e. the inserted energy is finite being
appropriately space-collimated. Our objective is to confirm that the solution (4.40) has all the
common characteristics inherent to EM waves such as the capability to transfer energy in space-
time domain with light velocity, periodical amplitude variation, polarization, etc.
X-axis

Wave Magnitude Direction of Propagation Direction of Propagation

< 0 Origin > 0
Z-axis Z-axis
Figure 4.1.3 Solution (4.40) illustration at successive time steps

Let us refer to Figure 4.1.3 representing the solution (4.40) at successive time steps ≥ 0, =

0,1, … ,4.