Page 194 - Maxwell House

174 Chapter 4

1. The initial energy pulse ( ) of unit amplitude, at the moment = 0 (shown in red) is
′

accompanied by right and left sets of the periodically repeating itself potentials: one is
( − )/2 (shown in green) and the second is ( + )/2 (shown in blue). It means

this excitation energy pulse breaks into two smaller ones of half-amplitude.
2. It takes the distance = + , where is some constant, for the right-side potential

( − )/2 to repeat itself while the left-side potential ( + )/2 repeats itself

each (− ) = − + . Clearly, each of these energy pulses not only repeats itself but

also transfers the energy portion from point to point creating the flux of energy over z-axis.
That is one of the main sign that this flux is EM wave;
3. The separation between two sequential points +1 and of equal magnitude is +1 −

= ( +1 − ). Therefore, the energy flux, aka EM wave, propagates over z-axis with

⁄
velocity ( +1 − ) ( +1 − ) = that is equal to the velocity of light in free-of-loss

homogeneous medium. That is the second important sign that this flux is EM wave. The
retarded or delayed nature of electromagnetic waves is clearly seen: the electromagnetic
phenomenon appears at the point with the time delay equals ( − )/ second.
′
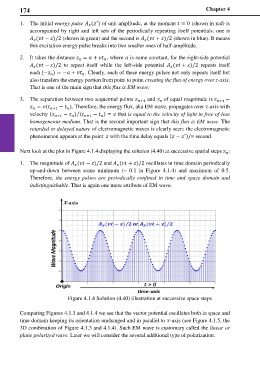
Next look at the plot in Figure 4.1.4 displaying the solution (4.40) at successive spatial steps :

1. The magnitude of ( − )/2 and ( + )/2 oscillates in time domain periodically

up-and-down between some minimum (~ 0.1 in Figure 4.1.4) and maximum of 0.5.
Therefore, the energy pulses are periodically confined in time and space domain and
indistinguishable. That is again one more attribute of EM wave.

Figure 4.1.4 Solution (4.40) illustration at successive space steps

Comparing Figures 4.1.3 and 4.1.4 we see that the vector potential oscillates both in space and
time domain keeping its orientation unchanged and in parallel to -axis (see Figure 4.1.5, the
3D combination of Figure 4.1.3 and 4.1.4). Such EM wave is customary called the linear or
plane polarized wave. Later we will consider the several additional type of polarization.