Page 200 - Maxwell House

180 Chapter 4

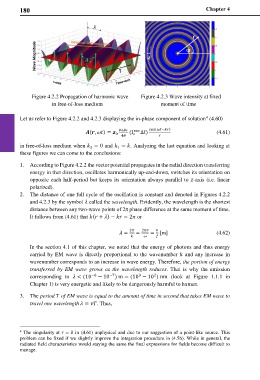
Figure 4.2.2 Propagation of harmonic wave Figure 4.2.3 Wave intensity at fixed
in free-of-loss medium moment of time

4
Let us refer to Figure 4.2.2 and 4.2.3 displaying the in-phase component of solution (4.60)
0 cos (−)
(, ) = 0 ( ∆) (4.61)
4
in free-of-loss medium when = 0 and = . Analyzing the last equation and looking at
2 1
these figures we can come to the conclusions:
1. According to Figure 4.2.2 the vector potential propagates in the radial direction transferring
energy in that direction, oscillates harmonically up-and-down, switches its orientation on
opposite each half-period but keeps its orientation always parallel to -axis (i.e. linear
polarized).
2. The distance of one full cycle of the oscillation is constant and denoted in Figures 4.2.2
and 4.2.3 by the symbol called the wavelength. Evidently, the wavelength is the shortest
distance between any two-wave points of 2π phase difference at the same moment of time.
It follows from (4.61) that ( + ) − = 2 or

2 2
= = = [m] (4.62)

In the section 4.1 of this chapter, we noted that the energy of photons and thus energy
carried by EM wave is directly proportional to the wavenumber and any increase in
wavenumber corresponds to an increase in wave energy. Therefore, the portion of energy
transferred by EM wave grows as the wavelength reduces. That is why the emission
2
−7
3
corresponding to < (10 −6 − 10 ) m = (10 − 10 ) nm (look at Figure 1.1.1 in
Chapter 1) is very energetic and likely to be dangerously harmful to human.
3. The period of EM wave is equal to the amount of time in second that takes EM wave to
travel one wavelength = . Thus,

4 The singularity at = 0 in (4.61) unphysical and due to our suggestion of a point-like source. This
problem can be fixed if we slightly improve the integration procedure in (4.56). While in general, the
radiated field characteristics would staying the same the final expressions for fields become difficult to
manage.