Page 41 - Contenidos temáticos Ciencias Naturales

P a g e | 36

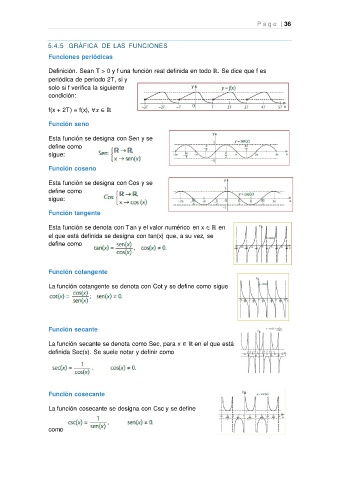
5.4.5 GRÁFICA DE LAS FUNCIONES

Funciones periódicas

Definición. Sean T > 0 y f una función real definida en todo ℝ. Se dice que f es
periódica de período 2T, si y
solo si f verifica la siguiente
condición:

f(x + 2T) = f(x), ∀ ∈ ℝ

Función seno

Esta función se designa con Sen y se
define como
sigue:

Función coseno

Esta función se designa con Cos y se
define como
sigue:

Función tangente

Esta función se denota con Tan y el valor numérico en x ∈ ℝ en
el que está definida se designa con tan(x) que, a su vez, se
define como

Función cotangente

La función cotangente se denota con Cot y se define como sigue

Función secante

La función secante se denota como Sec, para x ∈ ℝ en el que está
definida Sec(x). Se suele notar y definir como

Función cosecante

La función cosecante se designa con Csc y se define

como