Page 10 - fonction bac 2023

2
3
g . ( ) x  x  3x  3x  1 : يلي امك ةفرعم دودح ريثك ةلاد g 7 :  نيرمت
. R ىلع g ةلادلا تاريغت سردأ 1 .

( ) 0
0;0.5  لاجملا ىلع  اديحو لاح لبقت g x  ةلداعملا ن أ نيب 2 .
. 0.125 هتعس لاجم يف  ـل ارصح طعا 3 .
R . ىلع g ةلادلا ةراشا جتنتسا 4 .

x  3x  3x  2
2
3

f ( ) x  : يلي امك R    1 ىلع ةفرعم ةيددع ةلاد f . II
 x   1 2
. ايسدنه جئاتنلا رسف مث فيرعتلا ةعومجم فارطأ دنع f ةلادلا تاياهن بسحأ 1 .

g ( ) x

f '( ) x  3 : نإف R    1 نم x ددع لك لجأ نم هنأ نيب 2 .
x   1

. اهتاريغت لودج لكشو f ةلادلا ريغت هاجتا جتنتسا مث
3
( ) 
f . ( )  ـل ارصح طعأ مث f  : ن أ نيب 3 .
   1 2

( 2)
. ايسدنه جئاتنلا رسف مث f (0) و f  بسحأ 4 .

C
  ـل ةبسنلاب لئام براقم ميقتسملا ( )  ـل ةلداعم نيع مث ، f ( ) x   1 1 نأ نيب 5 .
x
f
x   1 2
C
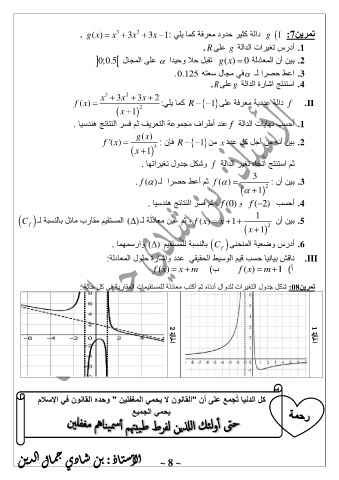
. امهمسراو ( )  ميقتسملل ةبسنلاب   ىنحنملا ةيعضو سردأ 6 .
f
:ةلداعملا لولح ةراشاو ددع يقيقحلا طيسولا ميق بسح اينايب شقان . III

f ( ) x  x m ) ب f ( ) x  m أ ) 1

داعم بتكأ مث
: ةلاح لك يف ةبراقملا تاميقتسملل ةل هاندأ لاودلل تاريغتلا لودج لكش : 08 نيرمت

1
2

لةالحا لةالحا

ملاسلإا يف نوناقلا هدحو " نيلفغملا يمحي لا نوناقلا" نأ ىلع عمجُت ايندلا لك

عيمجلا يمحي

ب
ش ب تس
ن د لا لا مج يذا ن : ذا ألا

~ 8 ~