Page 5 - fonction bac 2023

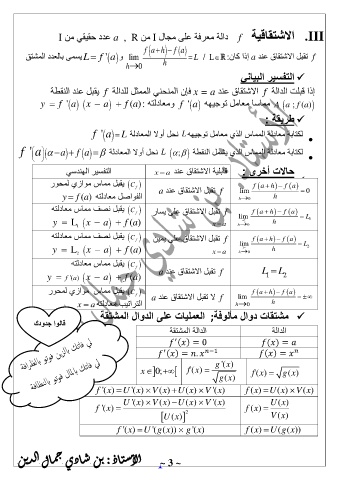
I نم يقيقح ددع a , R نم I لاجم ىلع ةفرعم ةلاد f ةيقاقتش لاا . III

 
قتشملا ددعلاب ىمسي L ' f a و lim f a h    f    a  L / L : ناك اذإ a دنع قاقتشلاا لبقت f
h 0 h

ينايبلا ريسفتلا 

ةطقنلا دنع لبقي f ةلادلل لثمملا ينحنملا نإف x = a دنع قاقتشلاا f ةلادلا تلبق اذإ
  
 


y 
a 
x 
( )
' f a f a : هتلداعمو ' f a ههيجوت لماعم اسامم A a f 
; ( ) a

: ةقيرط 
 
' f a  L ةلداعملا لاوأ لح L ن ههيجوت لماعم يذلا سامملا ةلداعم ةباتك ل


' f a         a  f a      ةلداعملا لاوأ لح  ;  L ن   ةطقنلا لمشي يذلا سامملا ةلداعم ةباتك ل 
يسدنهلا ريسفتلا x  a دنع قاقتشلاا ةيلباق : ىرخأ تلااح
روحمل يزاوم سامم لبقي    f a h   f   a 
C

f
lim
y  f ( ) a هتلداعم لصاوفلا a دنع قاقتشلاا لبقت f h 0 h  0
هتلداعم سامم فصن لبقي   راسي ىلع قاقتشلاا لبقت f f a h   f   a
C

f
lim

y 
L x  a   ( f ) a x a h 0 h  L 1

1
هتلداعم سامم فصن لبقي   نيمي ىلع قاقتشلاا لبقت f  f a h   f   a
C

f
lim

y 
L x  a   ( f ) a x a h 0 h  L 2

2
هتلداعم سامم لبقي   L  L
C
f


y 
'( ) ( f a
f a x  a  ) a دنع قاقتشلاا لبقت f 1 2
روحمل يزاوم سامم لبقي   a دنع قاقتشلاا لبقت لا f lim  f a h   f   a  

C
f
x  a هتلداعم بيتارتلا h 0 h

ةقتشملا لاودلا ىلع تايلمعلا ; ةفولأم لاود تاقتشم 
كدودج اولاق
ةقتشملا ةلادلا ةلادلا
′
( ) = 0 ( ) =
′

( ) = . −1 ( ) =
x

x
x 0; f '( )  g '( ) ' f ( ) x  g ( ) x
g ( )
x




x
x
x
x
f '( ) U '( ) V ( ) U ( ) V '( ) f ( ) x  U ( ) x  V ( ) x
x



x
U '( ) V ( ) U ( ) V '( ) U ( )
x
x
x
x
x
f '( )  f ( ) 
x
x
 ( )U x  2 V ( )


x
x
x
x
f '( ) U '( ( ))  g x g '( ) f ( ) U ( ( ))
g

ب
ش ب تس
ن د لا لا مج يذا ن : ذا ألا

~ 3 ~