Page 652 - Krugmans Economics for AP Text Book_Neat

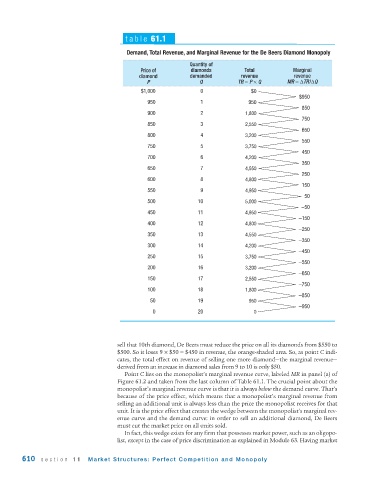
table 61.1

Demand, Total Revenue, and Marginal Revenue for the De Beers Diamond Monopoly

Quantity of
Price of diamonds Total Marginal
diamond demanded revenue revenue
P Q TR = P × Q MR =ΔTR/ΔQ
$1,000 0 $0
$950
950 1 950
850
900 2 1,800
750
850 3 2,550
650
800 4 3,200
550
750 5 3,750
450
700 6 4,200
350
650 7 4,550
250
600 8 4,800
150
550 9 4,950
50
500 10 5,000
−50
450 11 4,950
−150
400 12 4,800
−250
350 13 4,550
−350
300 14 4,200
−450
250 15 3,750
−550
200 16 3,200
−650
150 17 2,550
−750
100 18 1,800
−850
50 19 950
−950
0 20 0

sell that 10th diamond, De Beers must reduce the price on all its diamonds from $550 to
$500. So it loses 9 × $50 = $450 in revenue, the orange-shaded area. So, as point C indi-
cates, the total effect on revenue of selling one more diamond—the marginal revenue—
derived from an increase in diamond sales from 9 to 10 is only $50.
Point C lies on the monopolist’s marginal revenue curve, labeled MR in panel (a) of
Figure 61.2 and taken from the last column of Table 61.1. The crucial point about the
monopolist’s marginal revenue curve is that it is always below the demand curve. That’s
because of the price effect, which means that a monopolist’s marginal revenue from
selling an additional unit is always less than the price the monopolist receives for that
unit. It is the price effect that creates the wedge between the monopolist’s marginal rev-
enue curve and the demand curve: in order to sell an additional diamond, De Beers
must cut the market price on all units sold.
In fact, this wedge exists for any firm that possesses market power, such as an oligopo-
list, except in the case of price discrimination as explained in Module 63. Having market

610 section 11 Market Structures: Perfect Competition and Monopoly