Page 21 - complejos

6 6 6 # # #

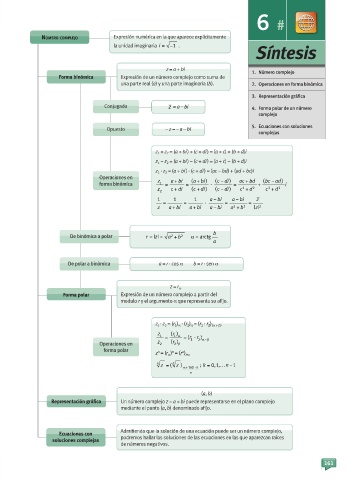
Número complejo Expresión numérica en la que aparece explícitamente
Síntesis
Síntesis
Síntesis
la unidad imaginaria i = −1 .
z = a + bi
Númer
.

1 1. Polinomioso complejo
Forma binómica Expresión de un número complejo como suma de
una parte real (a) y una parte imaginaria (b). 2 2. Factorización de polinomios aciones en forma binómica
.
Oper

.
epr
esentación gráfica

R
3 3. Fracciones algebraicas
Conjugado z = a – bi 4. Forma polar de un número
complejo
Opuesto – z = – a – bi 5. Ecuaciones con soluciones
complejas
z 1 + z 2 = (a + bi ) + (c + di ) = (a + c) + (b + d)i
z 1 - z 2 = (a + bi ) - (c + di ) = (a + c) - (b + d)i
z 1 · z 2 = (a + bi ) · (c + di ) = (ac - bd) + (ad + bc)i
Operaciones en
forma binómica z 1 = a + bi = (a + bi) · (c − di) = ac + bd + (bc − ad) i
2
2
z 2 c + di (c + di) (c − di) c + d 2 c + d 2
1 = 1 = 1 · a − bi = a − bi = z
z a + bi a + bi a − bi a + b 2 |z| 2
2

b
De binómica a polar r = |z| = a + b 2 α = arctg
2
a

De polar a binòmica a = r · cos a b = r · sen a

z = r a
Forma polar Expresión de un número complejo a partir del
modulo r y el argumento a que representa su afijo.

z 1 · z 2 = (r 1 ) a · (r 2 ) a = (r 1 · r 2 ) (a + b)
z (r )
1 = 1 α = (r · r )
1
2 α−β
Operaciones en z 2 (r )
2 β
forma polar n n n
z = (r a ) = (r ) na
n z = ( z ) α+360 · k ; k = 0,1,…n −1
n
n

(a, b)
Representación gráfica Un número complejo z = a + bi puede representarse en el plano complejo
mediante el punto (a, b) denominado afijo.

Ecuaciones con Admitiendo que la solución de una ecuación puede ser un número complejo,
soluciones complejas podremos hallar las soluciones de las ecuaciones en las que aparezcan raíces
de números negativos.

161
161